Hace algunas semanas compré por Ebay 3 módulos ESP8266 con la esperanza de poder utilizarlos en aplicaciones de IoT. Oí hablar de este módulo en Hackaday y solo leer de lo que era capaz no me lo pensé dos veces:
- Procesador con puertos GPIO (General Purpose Input Output)
- Wifi integrado
- ¡Solo vale 4€! (Actualización: actualmente es posible encontrarlo por ~1.5€)
Por tanto, este chip es capaz de conectarse con la red Wifi de tu casa, guardar o escribir información en una base de datos, hacer las veces de servidor, leer información de sensores, activar otros actuadores (como relés)… ¡Las posibilidades son enormes! Es un pequeñísimo Arduino con Wifi integrado.
Los primeros meses desde la salida del ESP8266 fueron bastante oscuros, ya que no se tenía apenas información, no había un SDK oficial y lo que había estaba en chino.
Pero recientemente la comunidad ESP8266 ha empezado a florecer ofreciendo diferentes vertientes por las que poder configurarlo. Yo me voy a centrar únicamente en la que utiliza el firmware NodeMCU.
Este firmware hace correr un compilador de LUA en el procesador, de manera que podremos escribir los programas que queramos correr en este mismo lenguaje.
Para poder instalar el firmware solo hay que conectar un FTDI (USB-UART converter) a nuestro ESP8266 de la siguiente manera:
Advertir que es obligatorio alimentar el ESP8266 a 3.3V, ya que por lo contrario quemaréis el chip.
Para entrar en modo de escritura de firmware hay que conectar el pin GPIO0 a masa. Yo he utilizado un jumper con que puedo conectar y desconectar fácilmente el pin.
Cuando tengamos este montaje hecho, necesitaremos descargar el grabador del firmware, que lo podemos encontrar también en el GitHub de NodeMCU.
Una vez descargado, abrimos el flasher:
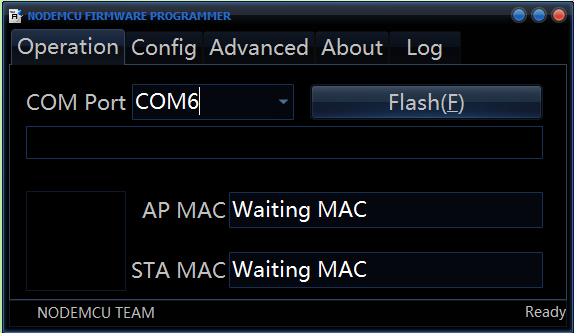
Con lo que nos aperecerá la siguiente aplicación:
Automáticamente cuando conectemos nuestro FTDI cambiará el puerto COM. Si no te sucede asegúrate de tener los drivers para tu FTDI instalados.
Flashear el ESP8266 con NodeMCU es tan sencillo como darle al botón Flash(F), y se pondrá a escribir el firmware en la memoria del procesador. Como se puede ver en la pestaña Config hace cuatro escrituras distintas, siendo la tercera la que más tiempo lleva. Cuando termine el FTDI se desconectará del equipo y aparecerá un símbolo verde abajo en la esquina izquierda. En mi caso dicho símbolo no ha aparecido pero el flasheo ha sido correcto igualmente.
Ahora que ya tenemos el firmware subido, tenemos que cargar nuestro programa. Para ello utilizaremos el programa LUAUploader de Hari Wiguna. Con esta aplicación especialmente desarrollada para el ESP8266 podremos subir nuestros programas de una manera muy sencilla.
Cabe destacar que la corriente que entrega un puerto USB del ordenador no es suficiente para iniciar el módulo de Wi-Fi, así que a partir de este momento es necesario alimentar el ESP8266 con una fuente externa. En mi caso he utilizado dos pilas LR03 (las pequeñas de los mandos) para obtener 3V. Recuerda que no sirven los 5V o el chip se quemará. Cuando conectes la fuente externa desconecta el pin de 3.3V del FTDI para evitar problemas, pero deja el pin de GND para unificar las masas del FTDI y de la fuente externa.
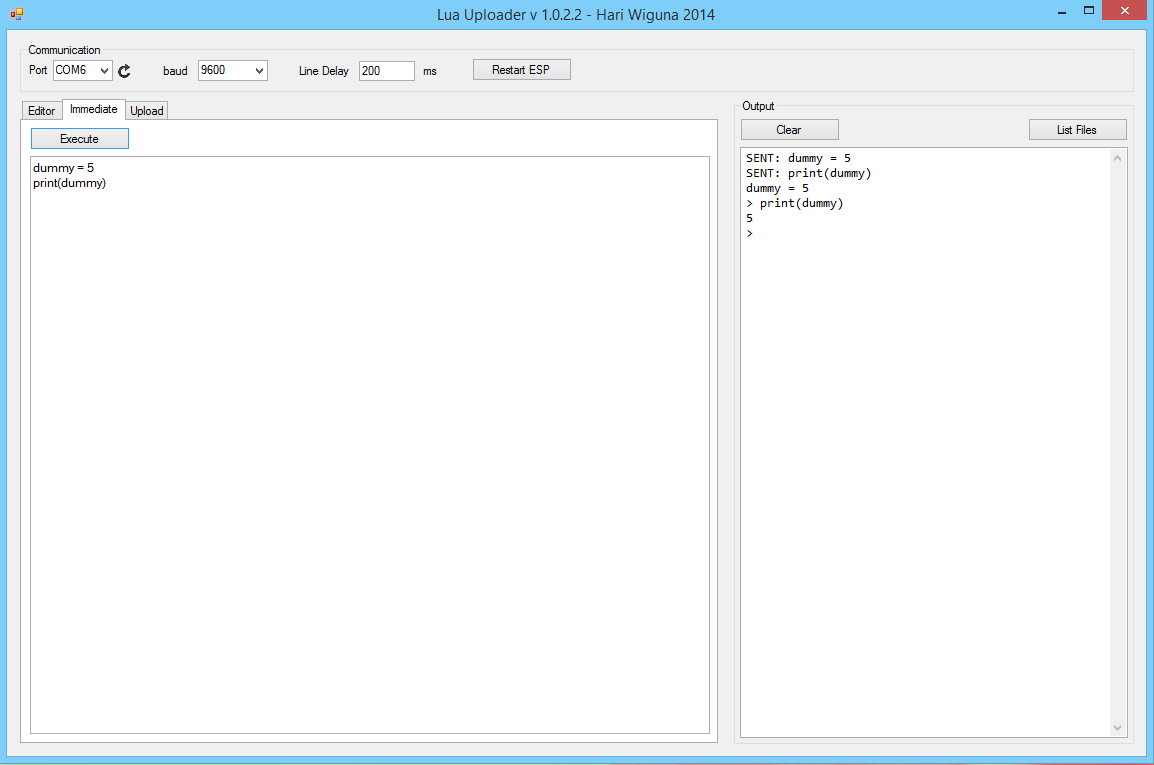
Una vez lo tengamos todo listo podemos pasar a lo divertido. Abrimos el LUAUploader y nos aparecerá la siguiente pantalla:
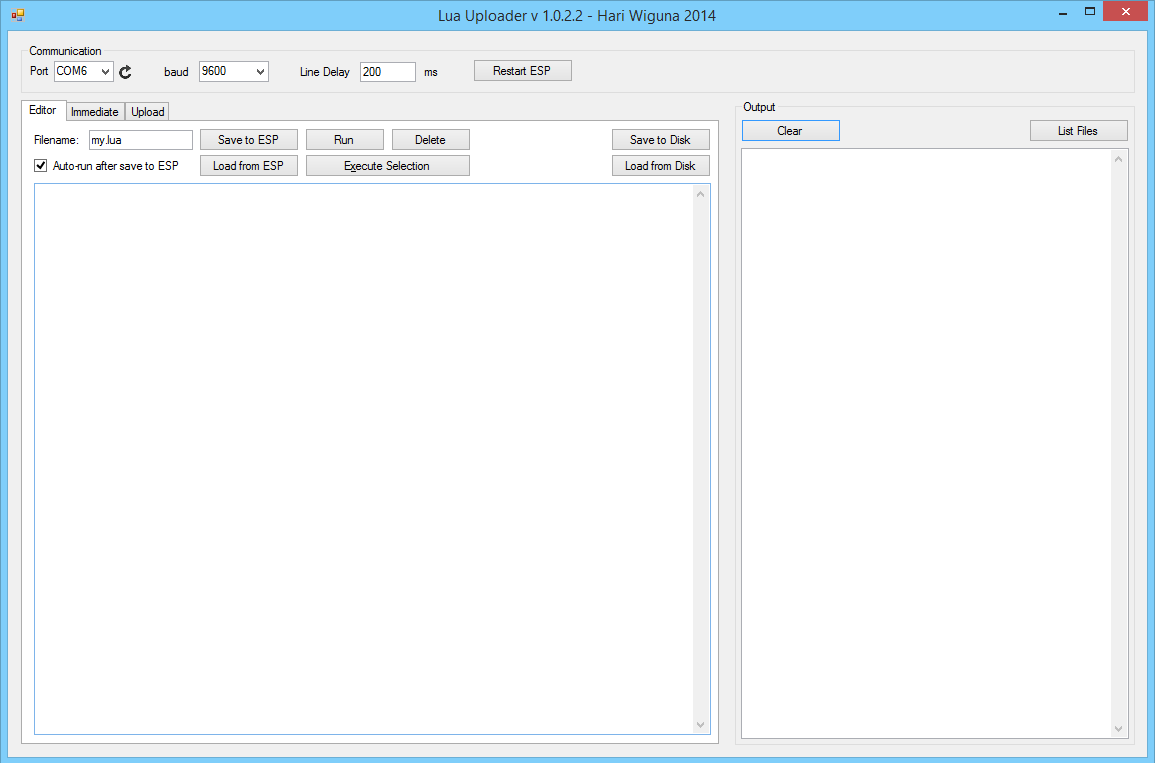 Para comprobar que el firmware ha sido grabado correctamente iremos a la pestaña “Immediate” y escribiremos un pequeño chunk de prueba (un chunk es cada trozo de código que Lua puede ejecutar)
Para comprobar que el firmware ha sido grabado correctamente iremos a la pestaña “Immediate” y escribiremos un pequeño chunk de prueba (un chunk es cada trozo de código que Lua puede ejecutar)
dummy = 5
print(dummy)Si el compilador nos devuelve 5, quiere decir que el firmware ha sido escrito correctamente:
Para poder conectarnos a nuestra red Wi-Fi es necesario introducir el siguiente chunk:
ip = wifi.sta.getip()
print(ip)
--nos devolverá nil
wifi.setmode(wifi.STATION)
wifi.sta.config("SSID","password")
ip = wifi.sta.getip()
print(ip)
--nos devolverá la IP asignadaHay veces que después de intentar conectarse a la red Wi-Fi continúa devolviendo nil. Probad a imprimir de nuevo la dirección IP con:
ip = wifi.sta.getip()
print(ip)Ahora, para hacer una pequeña prueba, podemos montar un servidor en el propio ESP8266 con el chunk:
srv=net.createServer(net.TCP)
srv:listen(80,function(conn)
conn:on("receive",function(conn,payload)
print(payload)
conn:send("<h1>Hola Ruben!</h1>")
end)
conn:on("sent",function(conn) conn:close() end)
end)Una vez subido, si accedemos a la dirección del ESP8266 nos devolverá la página con un heading y el texto “Hola Ruben!” (para poder escribir acentos hay que utilizar los códigos ASCII en HTML y utilizar la columna HTML Número: é = é)
Podéis encontrar muchos más ejemplos en el GitHub de NodeMCU.