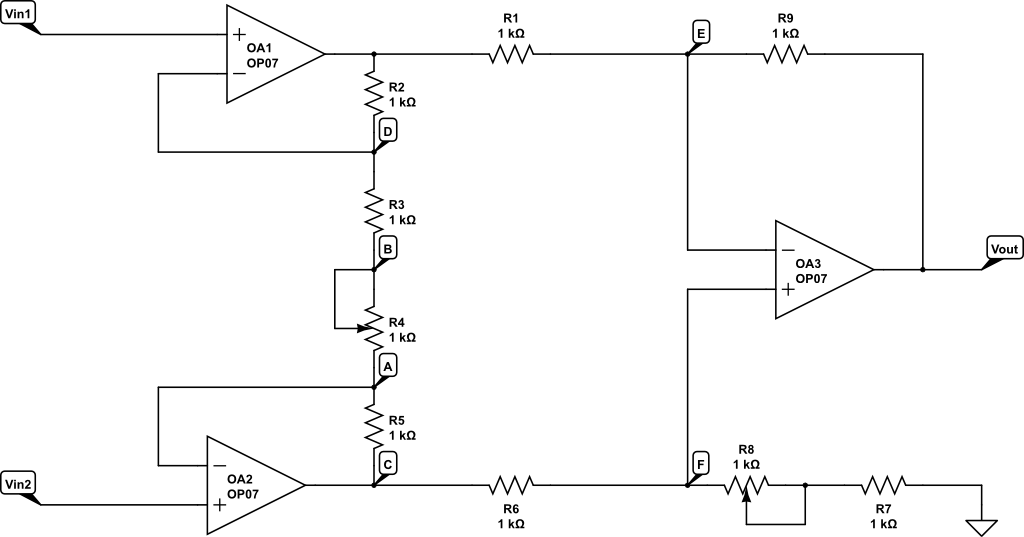
Amplificador de instrumentación con 3 AOEsta disposición de AI se puede separar en dos etapas:
Etapa 1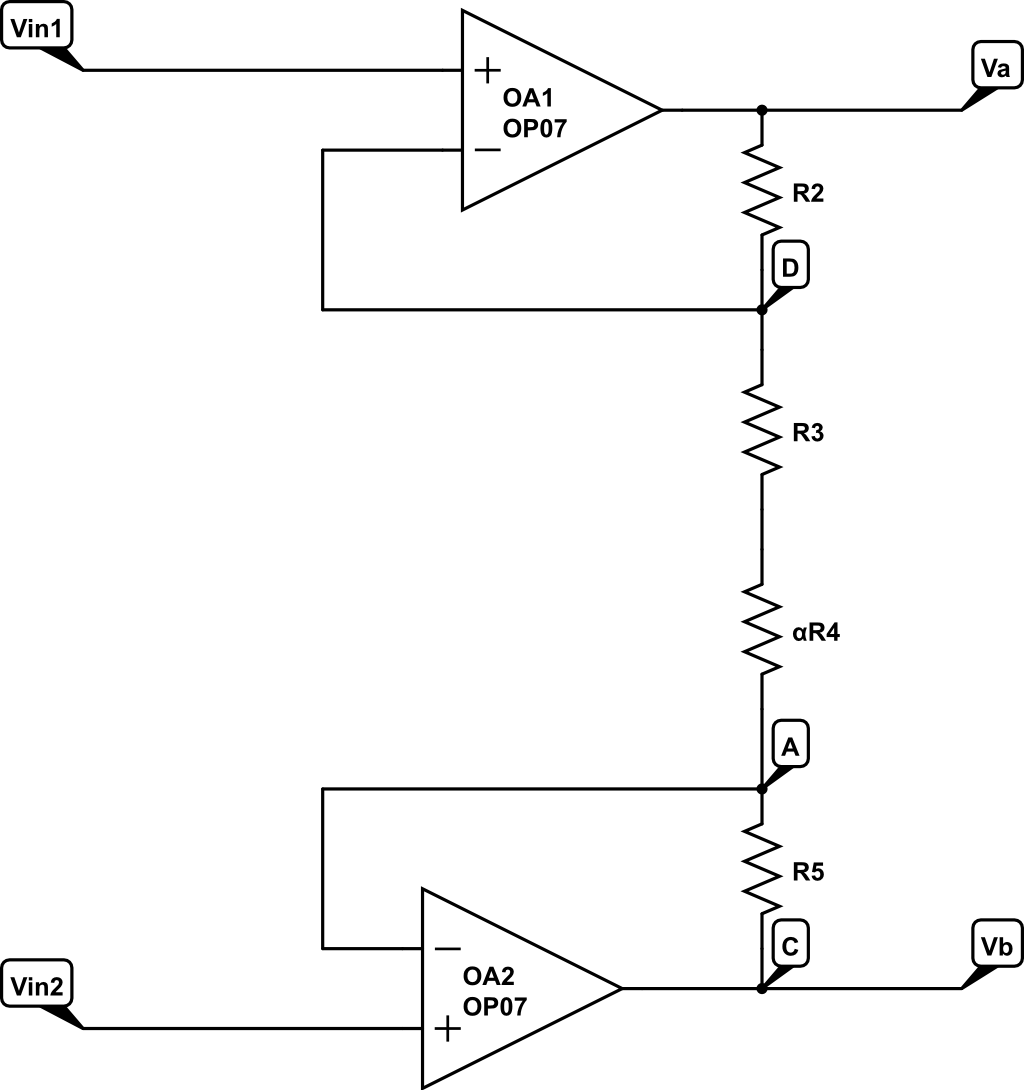 
Por superposición y haciendo el KCL:
\[ V_{in_1} = 0 \] \[R_3 + \alpha R_4 = R_G\] \[ \frac{V_{in_2}-V_B}{R_5} = \frac{0-V_{in_2}}{R_G}\] \[V_{in_2}R_G -V_B R_G =-V_{in_2}R_5\] \[V_B = \left( 1 + \frac{R_5}{R_G} \right) V_{in_2}\] \[\frac{0 – V_{in_2}}{R_G} + \frac{0 – V_A}{R_2} = 0\] \[V_A = – \frac{R_2}{R_G}V_{in_2}\]
Ahora con \(V_{in_2} = 0\),
\[\frac{V_{in_1}-0}{R_G} = \frac{0-V_B}{R_5} \] \[V_{in_1}R_5 =-V_B R_G\] \[V_B =-\frac{R_5}{R_G}V_{in_1}\] \[\frac{0 – V_{in_2}}{R_G} + \frac{0 – V_A}{R_2} = 0 \] \[V_A = \left( 1 + \frac{R_2}{R_G} \right) V_{in_1} \] Por lo que finalmente, tenemos que: \[V_A = \left( 1 + \frac{R_2}{R_G} \right) V_{in_1} – \frac{R_2}{R_G}V_{in_2} \] \[V_B = \left( 1 + \frac{R_5}{R_G} \right) V_{in_2} -\frac{R_5}{R_G}V_{in_1} \] En cuanto a la ganancia en modo común de esta etapa, la podemos calcular haciendo \(V_{in_1} = V_{in_2}\). De esta manera, \[V_A = \left( 1 + \frac{R_2}{R_G} \right) V_{in_1} – \frac{R_2}{R_G} V_{in_1} = V_{in_1}\] \[V_B = \left( 1 + \frac{R_5}{R_G} \right) V_{in_1} -\frac{R_5}{R_G}V_{in_1} = V_{in_1}\] Por tanto, sea cual sea el valor de \(R_2\), \(R_5\) y \(R_G\), la tensión en modo común pasa a los nodos \(V_A\) y \(V_B\).
La otra etapa restante es:
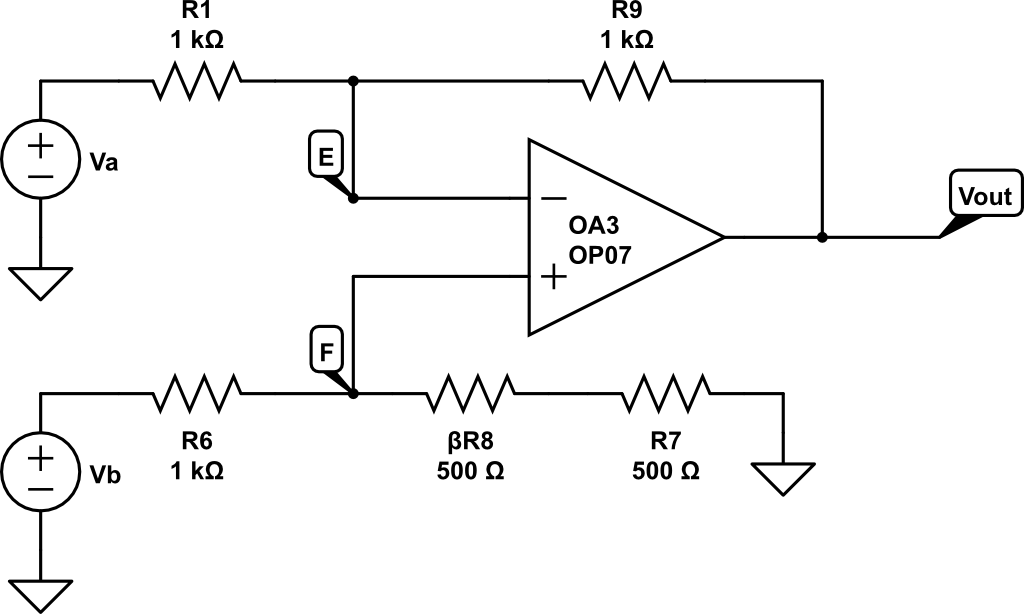De nuevo, aplicando superposición podemos llegar a la expresión final de la salida.
\[V_{out} = – \frac{R_9}{R_1} V_A + \left(1 + \frac{R_9}{R_1} \right) \frac{\beta R_8 + R_7 }{ \beta R_8 + R_7 + R_6} V_B \]
\[V_{out} = – \frac{R_9}{R_1} \left
+ \left(1 + \frac{R_9}{R_1} \right) \frac{\beta R_8 + R_7 }{ \beta R_8 + R_7 + R_6} \left
\[ \\left( 1 + \\frac{R\_5}{R\_G} \\right) V\_{in\_2} -\\frac{R\_5}{R\_G}V\_{in\_1} \\right\]\]
Para calcular la ganancia en modo común de esta etapa vamos a aplicar una tensión igual en las dos entradas diferenciales. Por tanto \(V_A = V_B = V_{CM}\). Así conseguimos la siguiente expresión para la tensión de salida. \[V_{out} = – \frac{R_9}{R_1} V_{CM} + \left(1 + \frac{R_9}{R_1} \right) \frac{\beta R_8 + R_7 }{ \beta R_8 + R_7 + R_6} V_{CM} \] También identificaremos \(R_{ref} = \beta R_8 + R_7\) para facilitar las operaciones. 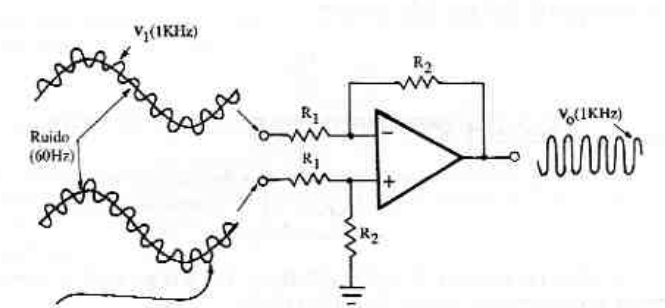\[V_{out} = – \frac{R_9}{R_1} V_{CM} + \left(1 + \frac{R_9}{R_1} \right) \frac{R_{ref}}{R_{ref}+ R_6} V_{CM} \] Idealmente, querríamos que esta tensión fuese igual a 0, de manera que el amplificador de instrumentación pudiese rechazar completamente para poder, por ejemplo, eliminar el ruido acoplado en ambas entradas tal y como puede verse en la figura.
\[V_{out} = – \frac{R_9}{R_1} V_{CM} + \left(1 + \frac{R_9}{R_1} \right) \frac{R_{ref}}{R_{ref}+ R_6} V_{CM} \] \[G_{cm} = \frac{V_{out}}{V_{CM} } = – \frac{R_9}{R_1} + \left(1 + \frac{R_9}{R_1} \right) \frac{R_{ref}}{R_{ref}+ R_6} \] \[G_{cm} = \frac{R_{ref}}{R_{ref}+R_6} – \frac{R_9 R_6}{R_1 R_{ref} + R_1 R_6} \] Por tanto, resolviendo la ecuación de ganancia en modo común igual a 0, \(G_{cm} = 0\), tenemos que \[- \frac{R_9}{R_1} + \left(1 + \frac{R_9}{R_1} \right) \frac{R_{ref}}{R_{ref}+ R_6} = 0\] Ecuación que podemos identificar de la siguiente manera: \[A = \frac{R_9}{R_1}\] \[ B =\frac{R_{ref}}{R_{ref}+ R_6}\] \[ – A + \left(1 + A \right) B = 0 \] \[-A + B + AB = 0 \] \[\left( B -1 \right) A = -B \] \[ A = \frac{-B}{B-1} = \frac{B}{1-B} \] \[A = \frac{\frac{R_{ref}}{R_{ref}+ R_6}}{1-\frac{R_{ref}}{R_{ref}+ R_6}} = \frac{R_{ref}}{R_6} \] \[\frac{R_9}{R_1} = \frac{R_{ref}}{R_6} \] Por tanto, para tener una ganacia en modo común de 0 (o lo que es lo mismo un CMRR\( = \infty\)), \(R_9 = R_{ref}\) y \(R_{1} = R_6\)
Por otra parte, si queremos que \(V_A = V_B\) cuando \(V_{in_1} = V_{in_2}\), necesitamos que se cumpla la siguiente relación entre las resistencias \(R_2\) y \(R_5\). \[ V_A = V_B \left( 1 + \frac{R_2}{R_G} \right) V_{in_1} – \frac{R_2}{R_G}V_{in_2} = \left( 1 + \frac{R_5}{R_G} \right) V_{in_2} -\frac{R_5}{R_G}V_{in_1} \left( 1 + \frac{R_2}{R_G} \right) – \frac{R_2}{R_G} = \left( 1 + \frac{R_5}{R_G} \right) -\frac{R_5}{R_G} \] Por simple inspección se llega a la conclusión de que \(R_2 = R_5\).
Por último, podemos calcular la ganancia diferencial y la ganancia de modo común de otro modo. Si definimos la tensión diferencial como \(V_d = V_{in_1}- V_{in_2}\) y la tensión en modo común como \(V_c = \frac{V_{in_1} + V_{in_2}}{2}\), sustituimos en la expresión de \(V_o\) e identificamos la expresión resultante como \(V_o = G_d V_d + G_c V_c\), en la que \(G_d\) es la ganancia diferencial y \(G_c\) es la ganancia en modo común (la misma que hemos calculado arriba, obtenemos que \(G_d\) es igual a: \[ G_d = \frac{-2 R_9 R_G R_{ref} – R_9 R_G R_6 – 2 R_9 R_2 R_{ref} -2 R_9 R_2 R_6 – R_{ref}R_1 R_G – 2 R_1 R_5 R_{ref} – 2 R_9 R_{ref} R_5}{2R_1 R_G \left( R_{ref} + R_6 \right) } \] En caso de tener las resistencias balanceadas, la expresión de la ganancia diferencial se simplifica a: \[G_d = -\frac{R_G^2}{R_1 \left( R_9 + R_1 \right)} – \frac{R_9}{2 \left( R_9 + R_1\right)} – \frac{R_9 R_2}{R_G \left( R_9 + R_1 \right)} – \frac{R_9}{2 \left( R_9+ R_1 \right)} – \frac{R_2 R_9}{R_G \left( R_9+ R_1 \right)} – \\ \frac{R_9^2 R_2}{R_1 R_G \left( R_9 + R_1 \right)} \]
Conclusiones
Este amplificador de instrumentación es muy utilizado para amplificar salidas de sensores y demás aplicaciones de instrumentación. Sus ventajas residen en que si está balanceado se puede conseguir tener una ganancia de modo común baja (o CMRR alto) a la vez que se mantiene una ganancia ajustable a través de \(R_G = R_3 + \alpha R_4\). Por último, también podemos ver como la impedancia de entrada de este amplificador es muy alta, ya que ambas entradas son las entradas de un AO. \[V_{out} = – \frac{R_9}{R_1} \left
\[ \\left( 1 + \\frac{R\_2}{R\_G } \\right) V\_{in\_1} – \\frac{R\_2}{R\_G }V\_{in\_2} \\right\]+\left(1 + \frac{R_9}{R_1} \right) \frac{R_{ref} }{R_{ref} + R_6} \left
\[ \\left( 1 + \\frac{R\_5}{R\_G} \\right) V\_{in\_2} -\\frac{R\_5}{R\_G}V\_{in\_1} \\right\]\] \[G_d = \frac{-2 R_9 R_G R_{ref} – R_9 R_G R_6 – 2 R_9 R_2 R_{ref} -2 R_9 R_2 R_6 – R_{ref}R_1 R_G – 2 R_1 R_5 R_{ref} – 2 R_9 R_{ref} R_5}{2R_1 R_G \left( R_{ref} + R_6 \right)} \] \[G_{cm} = \frac{R_{ref}}{R_{ref}+R_6} – \frac{R_9 R_6}{R_1 R_{ref} + R_1 R_6} \]
Enlaces a CircuitLab para simulación