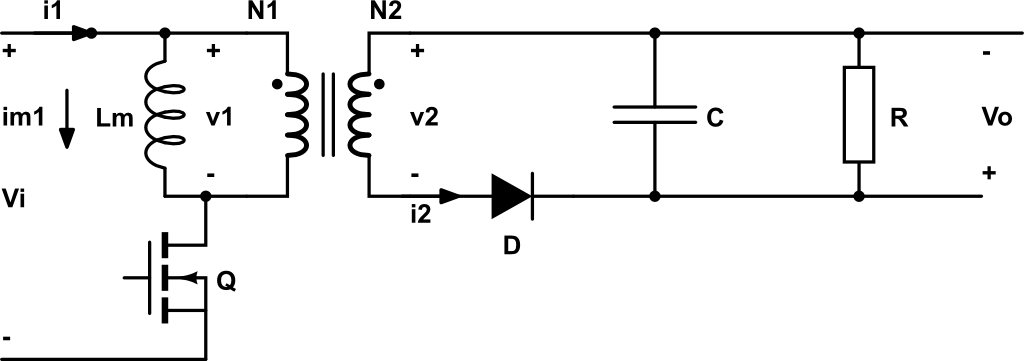
 Análisis en conducción continua
Análisis en conducción continua
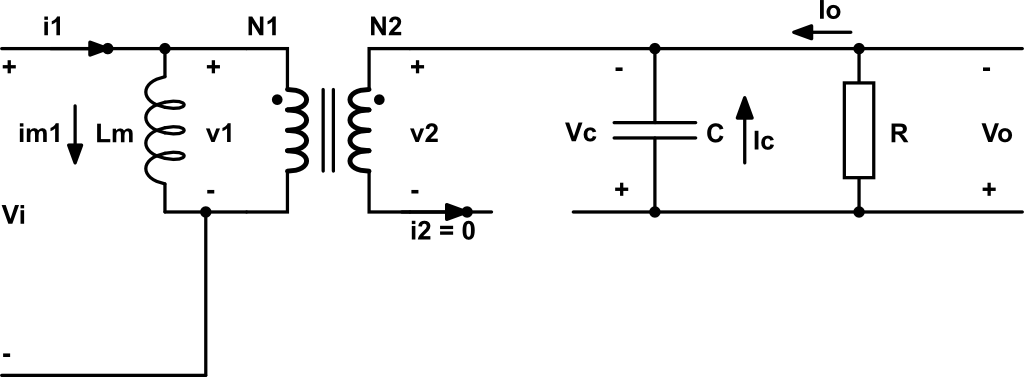
- Entre \(0 \leq t \leq D T_s\) Q: ON. \(i_1\) magnetiza el núcleo del transformador, por lo que genera un flujo magnético en el transformador. Este flujo magnético induce una tensión \(v_2\) que fuerza a que \(i_2\) tenga el sentido contrario al definido en el dibujo, es decir \(i_2 < 0\). Sin embargo, el diodo bloquea esta corriente, por que el diodo queda en circuito abierto (\(i_2 = 0\)).
En este caso, la tensión en el primario \(v_1\) es igual a \(V_i\).
\[v_1 = V_i = L_m \frac{di_{m1}}{dt} \Rightarrow \frac{di_{m1}}{dt} = \frac{V_i}{L_m} > 0 \rightarrow i_{m1} \text{ crece} \]
Despejando el diferencial de la corriente magnetizante del transformador:
\[ \int{\frac{di_{m1}}{dt} dt}= \int{\frac{V_i}{L_m} dt}\]
\[i_{m1}(t) = \frac{V_i}{L_m}t + I_{m_{min}} \]
\[v_2 = \frac{N_2}{N_1}v_1 = \frac{N_2}{N_1}V_i \]
\[ v_C = V_o\]
\[i_1 = i_{m1} + i_2 \cdot \frac{N_2}{N_1} = \left\{ i_2 = 0 \right\} = i_{m1}\]
\[i_2 = 0\]
\[i_c = C \frac{dv_0}{dt} = – I_o \Rightarrow \frac{dv_0}{dt} = -\frac{I_o}{C} \rightarrow V_o\text{ decrece}\]
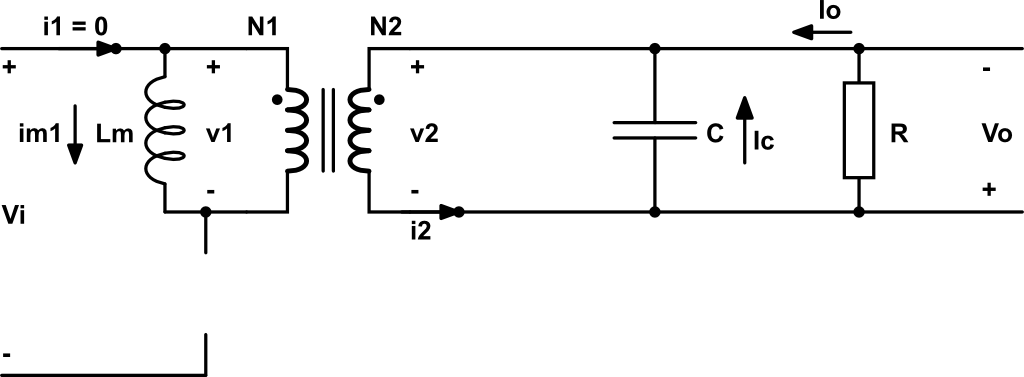
- Entre \(DT_s < t < T_s\). Q: OFF. El transistor está en circuito abierto y la corriente \(i_1 = 0\). La energía almacenada en el núcleo del transformador fuerza la conducción del diodo de salida debido a la corriente en sentido contrario que se induce de acuerdo con la ley de Lenz.
\[v_1 = \frac{N_1}{N_2}v_2 = L \frac{di_{m1}}{dt} = – \frac{N_1}{N_2} V_o \]
Despejando el diferencial de la corriente magnetizante del transformador:
\[ \int{\frac{di_{m}}{dt} dt} = \int{-\frac{N_1}{N_2}\frac{V_o}{L}dt} \]
\[ i_{m1}(t) = -\frac{N_1}{N_2} \frac{V_o}{L}\left( t-DT_s\right) + I_{m_{max}} \]
\[v_2 = -V_o \]
\[ v_c = V_o\]
\[ i_2 = i_c + I_o\]
\[ i_c = i_2 – I_0 = C \frac{dv_c}{dt} \]
De esta expresión, podemos despejar el diferencial de la tensión en el condensador. Solo es posible que el condensador se esté cargando en este periodo (\((1-D)T_s\)), por tanto, \(i_2 – I_o\) debe ser mayor que 0.
\[ \frac{dv_c}{dt} = \frac{i_2 – I_o}{C} > 0 \rightarrow v_c \text{ crece}\]
\[i_2 = \frac{N_1}{N_2}i_{m1}= \frac{N_1}{N_2} \left(-\frac{N_1}{N_2} \frac{V_o}{L}(t-DT_s) + I_{m_{max}} \right) = -\left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{L}(t-DT_s) + \left(\frac{N_1}{N_2}\right)^2 I_{m_{max}}\]
\[i_m(t)=\left\{\begin{matrix}\frac{V_i}{L}t+I_{m_{min}} &\text{si }0 < t < DT_s\\ -\frac{N_1}{N_2}\frac{V_o}{L}(t-DT_s)+I_{m_{max}} &\text{si }DT_s < t < T_s\end{matrix}\right. \]
Cómo calcular \(I_{2_{max}}\), \(I_{2_{min}}\), \(I_{1_{max}}\) y \(I_{1_{min}}\)
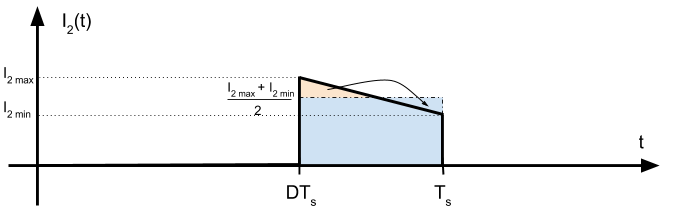
Para calcular \(I_{2_{max}}\) e \(I_{2_{min}}\) es necesario resolver un sistema de ecuaciones. La primera ecuación surge de considerar el nivel medio de \(i_2\).
 \[ \left< i_2 \right> = \left< i_c + I_o \right> = \left< I_o \right> = I_o\]
\[ \left< i_2 \right> = \left< i_c + I_o \right> = \left< I_o \right> = I_o\]
Como en media la corriente del condensador debe de ser 0 (de lo contrario la tensión en sus bornes tendería a infinito), obtenenos que el nivel medio de \(i_2\) es \(I_o\).
También podemos calcular el nivel medio de \(i_2\) como:
\[ \left< i_2 \right> = \frac{1}{T_s}\frac{I_{2_{max}}+I_{2_{min}}}{2}\left(1-D\right)T_s =\frac{I_{2_{max}}+I_{2_{min}}}{2}\left(1-D\right) \]
Por tanto, igualando ambas expresiones:
\[\frac{I_{2_{max}}+I_{2_{min}}}{2}\left(1-D\right) = I_o \]
Y reescribiéndola, tenemos la primera ecuación del sistema:
\[I_{2_{max}}+I_{2_{min}}= \frac{2\cdot I_o}{\left(1-D\right) } \]
Para la segunda hay que tener en cuenta que cuando Q=OFF, \(i_2\) es \(\frac{N_1}{N_2}\) veces la corriente \(i_{m1}\). Si recordamos, \(i_{m1}\) sale de plantear la ecuación de la tensión del primario \(v_1\):
\[v_1 = \frac{N_1}{N_2}v_2 = L \frac{di_{m1}}{dt}\]
Y integrando esta ecuación obtenemos:
\[ i_{m1}(t) = -\frac{N_1}{N_2} \frac{V_o}{L}\left( t-DT_s\right) + I_{m_{max}} \]
Por tanto,
\[i_2 = -\left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{L}\left( t-DT_s\right) + I_{2_{max}} \]
Esta ecuación nos dice cómo es la pendiente de \(i_2\). Por lo que podemos definir \(I_{2_{min}}\) como \(I_{2_{max}}\) menos la pendiente de \(i_2\) durante el periodo \((1-D)T_s\):
\[ I_{2_{min}} = I_{2_{max}} -\left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{L} \left(1-D\right)T_s\]
Si despejamos la expresión \( I_{2_{max}}-I_{2_{min}}\), obtenemos:
\[ I_{2_{max}} -I_{2_{min}} = \left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{L} \left(1-D\right)T_s\]
Con lo que ya podemos resolver el sistema de ecuaciones:
\[ \left.\begin{matrix}
I_{2_{max}}+I_{2_{min}}= \frac{2\cdot I_o}{\left(1-D\right) } \\ I_{2_{max}} -I_{2_{min}} = \left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{L} \left(1-D\right)T_s
\end{matrix}\right\} \]
Y de aquí despejamos:
\[ I_{2_{max}} = \frac{I_o}{1-D} + \left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{2L_m}\left(1-D\right)T_s\]
\[ I_{2_{min}} = \frac{I_o}{1-D} – \left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{2L_m}\left(1-D\right)T_s\]
Por último, teniendo en cuenta la ecuaciones que rigen el transformador, \(I_{1_{min}} = \frac{N_2}{N_1} I_{2_{min}}\) y \(I_{1_{max}} = \frac{N_2}{N_1} I_{2_{max}}\), por lo tanto:
\[ I_{1_{max}} = \frac{N_2}{N_1} \frac{I_o}{1-D} +\frac{N_1}{N_2} \frac{V_o}{2L_m}\left(1-D\right)T_s \]
\[ I_{1_{min}} = \frac{N_2}{N_1} \frac{I_o}{1-D} -\frac{N_1}{N_2}\frac{V_o}{2L_m}\left(1-D\right)T_s \]
También podemos escribir \(I_{1_{min}} \) e \(I_{1_{max}}\) en función de \(V_i\) sustituyendo \(V_o = \frac{N_2}{N_1}\frac{V_i D}{L}\).
\[ I_{1_{max}} = \frac{N_2}{N_1} \frac{I_o}{1-D} +\frac{V_i}{2L_m}D T_s \]
\[ I_{1_{max}} = \frac{N_2}{N_1} \frac{I_o}{1-D} -\frac{V_i}{2L_m}D T_s \]
Rizado de salida
Para calcular el rizado, hay que tener en cuenta la corriente del condensador ya que será el responsable de filtrar dicho rizado.
También vamos a considerar que la tensión de salida \(v_o\) está compuesta por la tensión DC y el rizado de la siguiente manera:
\[v_o = V_{o~DC} + v_{o~riz}\]
A priori ya podemos suponer, que cuanto mayor sea el valor de la capacidad C del condensador menor será el rizado.
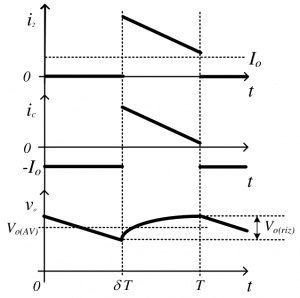
Cuando Q=ON, \(i_c = -I_o\).
Por lo que podemos integrar la corriente del condensador en el primer intervalo:
\[ v_c = \frac{1}{C}\int_0^{DT_s}{i_c(t) dt} = \frac{1}{C} \int_0^{DT_s}{-I_o dt} = – \frac{1}{C} I_o D T_s\]
De aquí, obtenemos que la variación del rizado es:
\[\Delta V_{o~riz} = \frac{1}{C} I_o D T_s \]
También hay que considerar que debido a la ESR del condensador, habrá una fuga en corriente que no irá hacia la carga sino que se quedará en el condensador. Esta tensión es:
\[V_{o~riz~(ESR)} = I_{2_{max}} \cdot ESR \]
Análisis de conducción discontinua
En conversor Flyback entra en conducción discontinua cuando el núcleo magnético del transformador se desmagnetiza. Esto ocurre cuando \(I_{mg_{min}}\) o su equivalente reflejado en el secundario \(I_{2_{min}}\) es 0.
\[I_{2_{min}} = 0 = \frac{I_o}{1-D} – \frac{N_1^2}{N_2^2}\frac{V_o}{2L} \left( 1 -D\right) T_s \]
En el periodo \(0 \leq t \leq D T_s\) el núcleo se magnetiza pero la energía que almacena no es la suficiente para que pasado el segundo periodo todavía quede algo de densidad de flujo magnético en el núcleo (magnetización). Por eso en el momento T’ del segundo periodo \(DT_s < t < T_s\), la corriente \(I_2\) se hace 0. Como tampoco hay tensión aplicada sobre el primario, la tensión en primario y secundario es 0.
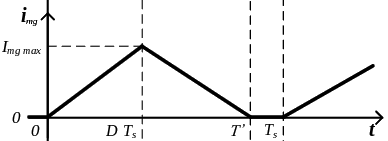
Para sacar la función de transferencia del conversor Flyback en conducción discontinua debemos resolver un sistema de ecuaciones. La primera ecuación la podemos encontrar haciendo la media de la tensión en el primario y despejando \(D_2\).
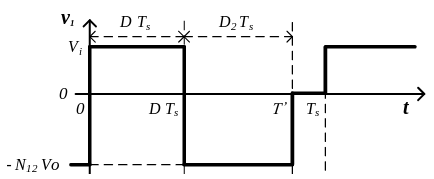
Como la media de la tensión en una bobina debe de ser 0, podemos encontrar la relación entre \(D_2\) y el resto de parámetros.
\[ \frac{1}{T_s} \left[V_i D T_s + \left(- \frac{N_1}{N_2} V_o D_2 T_s \right) \right] = 0 \]
\[ D_2 = \frac{V_i D}{N_{12} V_o } ~~~(1)\]
La otra ecuación la obtenemos de igualar la media de la corriente \(i_2\) con \(I_o\)
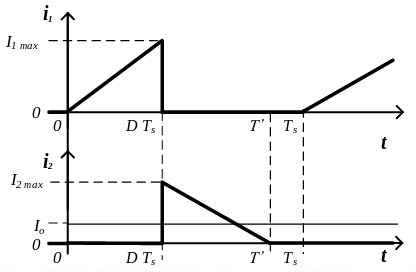
\[ I_o = \frac{V_o}{R} = \frac{1}{T_s} \left( D_2 T_s \frac{1}{2} N_{12} I_{mg_{max}} \right)~~~(2)\]
Al estar en conducción discontinua, \(I_{mg_{max}} \) es directamente:
\[I_{mg_{max}} = \frac{V_i}{L} D T_s ~~~(3)\]
Sustituyendo (1) y (3) en (2), obtenemos:
\[ V_o = \sqrt{\frac{R T_s}{2L}}D V_i = \sqrt{\frac{1}{2 \tau_s}} D V_i\]
En el que \(\tau_s\) es:
\[ \tau_s = \frac{L}{R T_s} \]
Por tanto, el conversor Flyback en conducción continua se comporta como un buck-boost en el que podemos conseguir tanto tensiones mayores como menores a la de entrada mientras que en conducción discontinua se comporta como un buck. Es decir, solo se pueden conseguir tensiones de salida menores a la de entrada.
Rizado de salida
En conducción discontinua el rizado de salida se calcula de la misma forma que en conducción continua, con la diferencia de que la corriente que pasa por el condensador ahora es menor. Por tanto, tanto el rizado debido a la capacidad como por la ESR es menor.
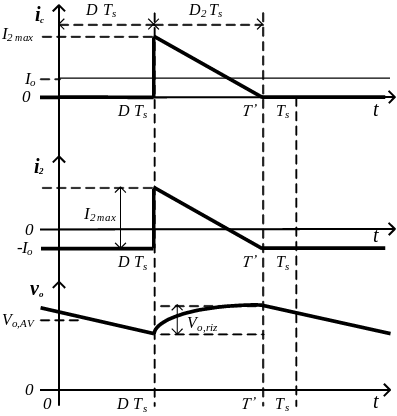
Como ya sabemos, \( i_c = i_2 – I_o\). Y la diferencia de tensión entre dos tiempos \(t_0\) y \(t_1\) es:
\[ \Delta v_c = \frac{1}{C} \int_{t_0}^{t_1}{i_c~dt} \]
Al estar en conducción discontinua podemos obtener fácilmente la expresión analítica de \(i_2\):
\[ i_2 = I_{2_{max}} – \frac{N_1^2}{N_2^2} \frac{V_o}{L} \left(t-DT_s\right) \]
Donde \( I_{2_{max}} \) es:
\[ I_{2_{max}} = \frac{N_1}{N_2} \frac{V_i}{L} D T_s \]
De \(i_2\) podemos obtener cuándo la corriente se hace 0, es decir T’:
\[i_2 = I_{2_{max}} – \frac{N_1^2}{N_2^2} \frac{V_o}{L} \left(T’-DT_s\right)=0 \]
\[ T’ = \left( \frac{V_i}{N_{12}} + 1\right) \frac{DT_s}{V_o} \]
Por tanto, ya podemos calcular el rizado de tensión debido a la capacidad:
\[ \Delta v_c = \frac{1}{C} \int_{DT_s}^{ \left( \frac{V_i}{N_{12}} + 1\right) \frac{DT_s}{V_o}}{\left[I_{2_{max}} – \frac{N_1^2}{N_2^2} \frac{V_o}{L} \left(t-DT_s\right) \right]~dt} \]
O de manera más sencilla, teniendo en cuenta los periodos en los que \(i_c = -I_o\).
\[ \Delta v_c = \frac{1}{C}\left( \int_{0}^{DT_s}{i_c~dt} + \int_{T’}^{T_s}{i_c~dt} \right) = \frac{1}{C}\left( \int_{0}^{DT_s}{-I_o} + \int_{T’}^{T_s}{-I_o} \right) \]
\[ \Delta v_c = \frac{1}{C} \left(-I_o\right) \left( DT_s + T_s – T’\right) \]
\[ \Delta v_c = \frac{1}{C} \left(-I_o\right) \left[ D + 1 – \left( \frac{V_i}{N_{12}} + 1\right) \frac{D}{V_o}\right]T_s \]