En anteriores entradas hemos definido el canal gaussiano, que es el más comúnmente usado para modelar los efectos del canal. Ahora vamos a definir otro parámetro del canal gaussiano: su capacidad.
Para ello supongamos que utilizamos un código de repetición de n bits con una modulación BPSK.
Si queremos enviar el símbolo A, transmitiremos el valor \(\sqrt{P}\) es la amplitud de los símbolos en la modulación BPSK.
Al enviar el símbolo de amplitud \(\sqrt{nP}\).
Por el criterio de mínima distancia (definida como la distancia euclídea), se puede calcular la probabilidad de error como:
\[P_e = Q\left( \frac{\frac{|| x_A – x_B||}{2}}{ \sigma}\right) = Q\left( \sqrt{\frac{nP}{\sigma^2} } \right)\]
Por tanto, podemos hacer que la probabilidad de error en este canal sea tan pequeña como queramos simplemente aumentando el número de repeticiones. Sin embargo, esto es una mala estrategia ya que la velocidad de transmisión decrece con n. Si necesitamos n usos del canal para poder enviar 1 solo bit, nuestra codificación deja mucho que desear.
La manera de minimizar la probabilidad de error sin tener que aumentar el número de repeticiones es distribuyendo las palabras del código de forma eficiente a lo largo del espacio de la señal. En dos dimensiones (tal y como la figura anterior) equivaldría a separar tanto como pudieramos las dos gaussianas. Sin embargo, cuando nuestro código lo conforman n bits, el espacio de la señal deja de ser en 2 dimensiones y pasa a ser de n dimensiones.
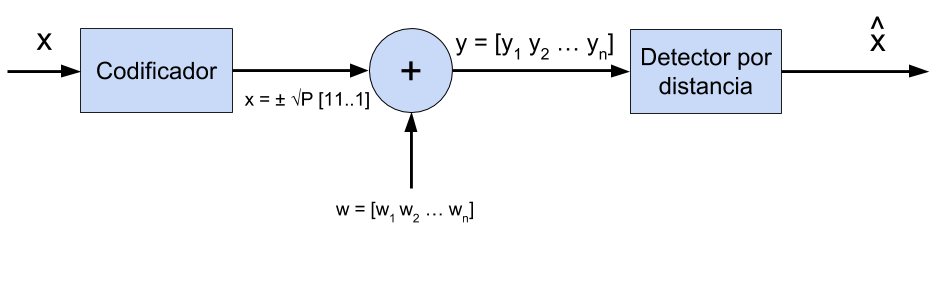
Como vemos en el diagrama anterior, cuando el código c que enviamos pasa a través del canal se le añade un ruido w. De este modo, a la salida del canal tenemos la señal y que es igual a la suma del código y del ruido: y = c + w
Según la ley de los grandes números, cuando el número de bits del código n tiende a infinito, la potencia del ruido tiende valer su varianza \(\sqrt{P}\)
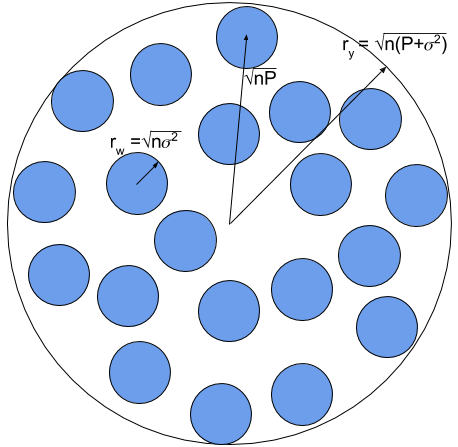
Por lo tanto, el código estará en un punto del hiperespacio Rn con distancia respecto al origen:
\[r_c = \sqrt{n P}\]
El ruido es aleatorio por lo que podría tener cualquier dirección del hiperespacio Rn y conforma una hiperesfera n-dimensional de radio:
\[r_w = \sqrt{n \sigma^2}\]
Así pues, cuando \(n \rightarrow \infty\), el vector y, que es la suma del código más el ruido del canal, estará en la superficie de una hiperesfera en Rn de radio ry:
\[r_y = \sqrt{n \left( P + \sigma^2 \right)}\]
Esta hiperesfera y con radio ry será la hiperesfera que englobe a todas las otras, ya que \(\sqrt{nP + \sigma^2}\) es la máxima amplitud que se puede enviar con la codificación de n repeticiones.
La comunicación será fiable siempre y cuando estas hiperesferas correspondientes para cada palabra código no se solapen. Teniendo esto en cuenta, el número máximo de palabras código que se podrán incluir dentro será la división entre el volumen de la mayor hiperesfera y el volumen de las hiperesferas de cada palabra codigo.
La superficie de una circunferencia es \(v_n = c_i r^n\). De este modo podemos definir esta relación de volumenes como:
\[\frac{V_y}{V_w} = \frac{r^n_y}{r^n_w} = \frac{\left( \sqrt{n\left( P + \sigma^2 \right)}\right)^n}{\left( \sqrt{n \sigma^2}\right)^n} = \left( 1+ \frac{P}{ \sigma^2} \right)^{\frac{n}{2}}\]
En consecuencia, si \(\left( 1+ \frac{P}{ \sigma^2} \right)^{\frac{n}{2}}\) es el número máximo de palabras código que caben en el espacio de la señal, el número máximo de bits por uso de canal que pueden ser transmitidos fielmente o con una probabilidad de error tan pequeña como se quiera por este canal será:
\[C = \underbrace{\frac{1}{n}}_{\text{cuantas veces uso el canal}} \underbrace{\log{ \left( 1+ \frac{P}{ \sigma^2} \right)^{\frac{n}{2}} }}_{\text{numero de bits necesarios para representar todos los simbolos}} = \frac{1}{n} \frac{n}{2} \log{ \left( 1+ \frac{P}{ \sigma^2} \right)} = \frac{1}{2} \log{ \left( 1+ \frac{P}{ \sigma^2} \right)}\]
Por lo que finalmente, la capacidad del canal AWGN es:
\[C =\frac{1}{2} \log{ \left( 1+ \frac{P}{ \sigma^2} \right) }\]
En el caso de canales complejos limitados en banda, podemos expresar la capacidad a partir del ancho de banda del canal B. El periodo del símbolo es el mismo que el tiempo de uso del canal, que equivale a \(\sigma^2 = N_0 B\). De esta manera, la expresión queda:
\[C =B \log{ \left(1 + \frac{P}{ \sigma^2 }\right) } = B \log{ \left( 1 + \frac{P}{N_0 B} \right) }= B \log{\left( 1 + SNR \right) }~~bits/s\]
Observaciones de la capacidad del canal gaussiano
- Si la SNR es 0, la capacidad del canal también es 0.
- La capacidad tiende a infinito si el ancho de banda B permanece constante y la SNR tiende a infinito, lo que significa que las comunicaciones sin ruido permiten tasas de transmisión infinitas.
- Cuando el ancho de banda tiende a infinito:
\[C_{\infty} = \lim_{B \rightarrow \infty} \left[ B \log{ \left(1 + \frac{P}{ \sigma^2 } \right) } \right] \underbrace{=}_{\ln_e x = \frac{log_2 x}{log_2 e}} \\ = log_2 \left( e \right) \lim_{B \rightarrow \infty} \left[ B \ln{ \left( 1 + \frac{P}{ \sigma^2 } \right)} \right] \underbrace{=}_{l’H\hat{o}pital} \\ = \log_2{ \left( e \right) } \frac{P}{N_0} = 1.44 \frac{P}{N_0}\]
Por tanto, la máxima capacidad que podemos tener es \(C_\infty T_b = 1\),
\[C_\infty T_b = 1.44 \frac{P T_b}{N_0} = 1.44 \frac{E_b}{N_0} = 1 \Rightarrow \left. \frac{E_b}{N_0} \right|_{\text{min}} = \\ = \frac{1}{1.44} = 0.69 = -1.59~dB\]
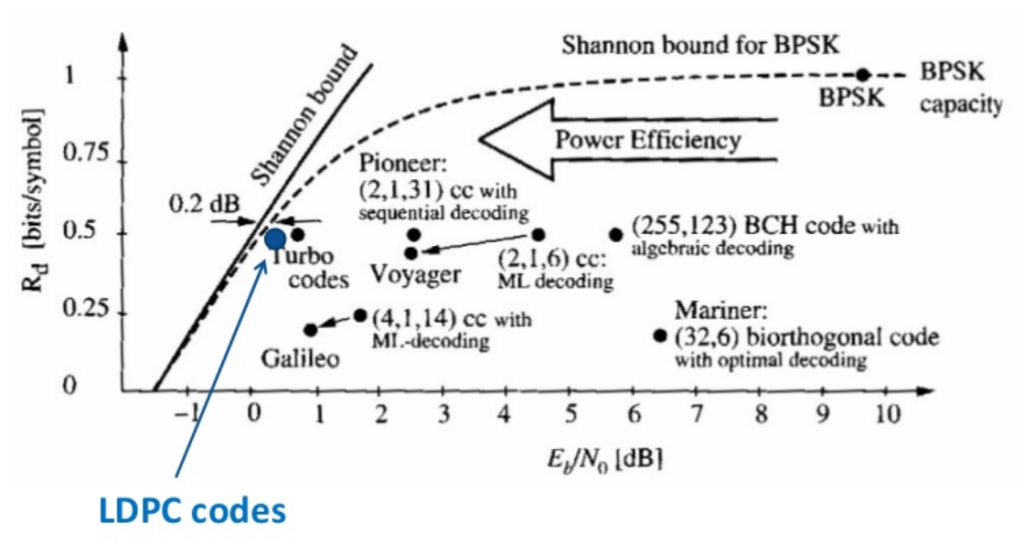
que es el llamado límite de Shannon. Es la mínima relación entre la energía del bit y la densidad espectral de potencia del ruido a la que podemos transmitir.
