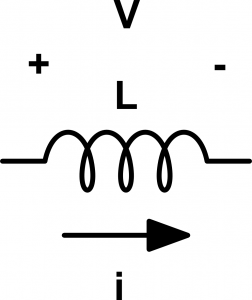
\[V_L(t) = L \frac{di(t)}{dt} \]
Si despejamos el diferencial e integramos:
\[\frac{di(t)}{dt} = \frac{V_L}{L}\]
\[\int{\frac{di(t)}{dt} dt} = \int{\frac{V_L}{L} dt}\]
\[ i(t) = \int{\frac{V_L}{L} dt} = i(0) + \frac{V_L}{L}t \]
La variación de la corriente en el tiempo no puede ser instantánea, ya que de lo contrario habría un pico infinito de tensión en el inductor (\(v(t) = \infty\)).
\[ \frac{di(t)}{dt} \neq \infty \]
Si el valor de la inductancia L es grande, las variaciones de corriente en el inductor serán pequeñas, por lo que el inductor se podrá considera como una fuente de corriente.
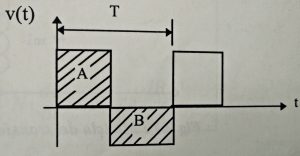
En régimen permanente, el valor medio de la tensión en los extremos del inductor debe ser nulo, ya que de lo contrario la corriente en bornes del inductor aumenaría hasta el infinito.
Es decir, ya que:
\[ i(t) = \int_0^t{-\frac{v_L(t)}{L} dt} \]
si \(v_L(t)\) no tuviese una media nula, la integral de la tensión sería infinito, ya que solo sumaría.
Por tanto:
\[<v(t)> = \frac{1}{T} \int_0^T v(t) dt = 0\]