El canal gaussiano se utiliza para modelar la amplia mayoría de casos reales en comunicaciones. A diferencia de los canales vistos anteriormente como el canal borrador o canal simétrico, el canal gaussiano es continuo. Este canal también es conocido como canal AWGN (Additive White Gaussian Noise Channel), en la que el ruido se modelo mediante una variable aleatoria gaussiana w, con media 0 y varianza \(\sigma^2\).
Una manera de poder detectar a la salida del canal los mensajes de la fuente, es mediante un detector por umbral.
 Si transmitimos símbolos BPSK de amplitudes ±A, las funciones de verosimilitud \(p_y \left( y | x = A \right)\) y \(p_y \left( y | x = -A \right)\) son gaussianas de media ±A y varianza \(\sigma^2\)
Si transmitimos símbolos BPSK de amplitudes ±A, las funciones de verosimilitud \(p_y \left( y | x = A \right)\) y \(p_y \left( y | x = -A \right)\) son gaussianas de media ±A y varianza \(\sigma^2\)
Para decidir si se ha enviado un 1 ó un 0, se utiliza el criterio de mínima distancia, de manera que si los símbolos equiprobables basta con saber si están a la derecha o izquierda del origen de coordenadas para decirdir si son un 1 ó un 0 respectivamente.
Función Q
La función Q es una función que calcula la integral de una gaussiana, de manera que la podemos aprovechar aquí para calcular el error de símbolo en la función de distribución de probabilidad.
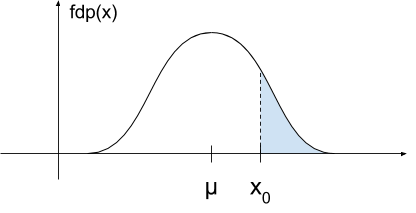
Si tenemos una función de probabilidad gaussiana con media \(\mu\), su expresión es:
\[p\left( x\right) = \frac{1}{\sigma \sqrt{2 \pi }}e^{-\frac{\left( x – \mu \right)^2}{2 \sigma^2}}\]
Si queremos saber la probabilidad que hay desde \(\mu + x_0\) hasta \(\infty\), la expresión utilizando la función Q es:
\[P\left( X > x_0 \right) = Q \left( \frac{ x_0 – \mu}{\sigma} \right)\]
De esta manera podemos calcular la probabilidad de error que se comete mediante el uso de detección por umbral:
\[P_e = Q \left( \frac{A}{\sigma} \right)\]
AWGN: Ruido Blanco Gaussiano Aditivo.
Así es como se considera el ruido en los sistemas de comunicación digital.
Gracias!