En los convertidores Flyback, debido a capacidad parásitas en los semiconductores y las inductancias de pérdidas del transformador aparecen una serie de oscilaciones y sobretensiones en los extremos del transistor y del diodo que puede llegar a los cientos de voltios con una alimentación de entrada de pocos voltios.
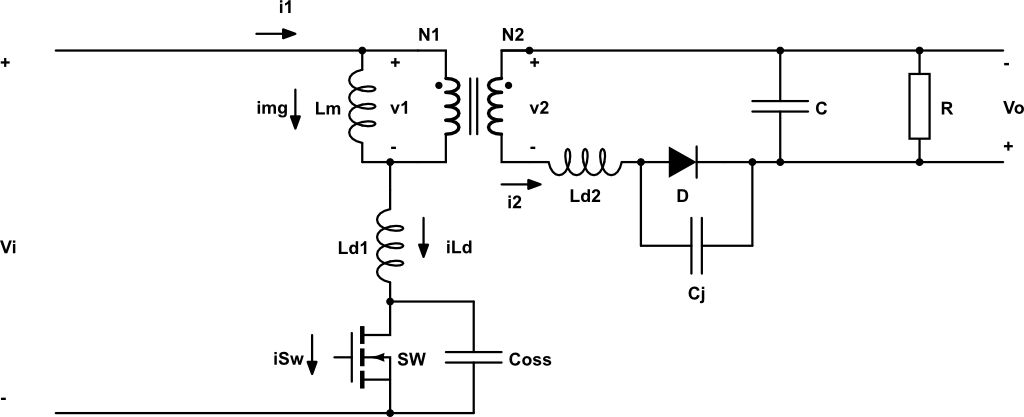
En el esquemático, \(L_{d_1}\) y \(L_{d_2}\) son las inductancias de pérdidas tanto del primario como del secundario, \(C_{oss}\) es la capacidad parásita del transistor y \(C_j\) la capacidad parásita del diodo.
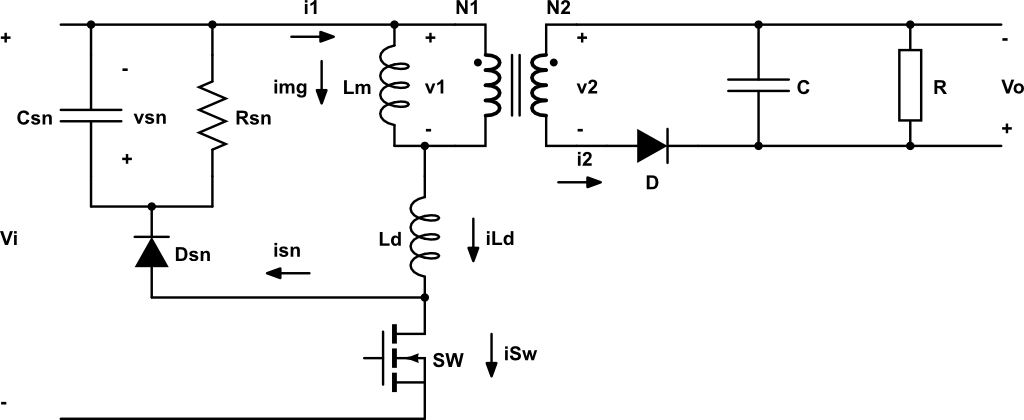
Para evitar las sobretensiones en la conmutación a OFF, existe una red snubber que reduce la tensión en el condensador. Consiste en un diodo, un condensador y una resistencia.
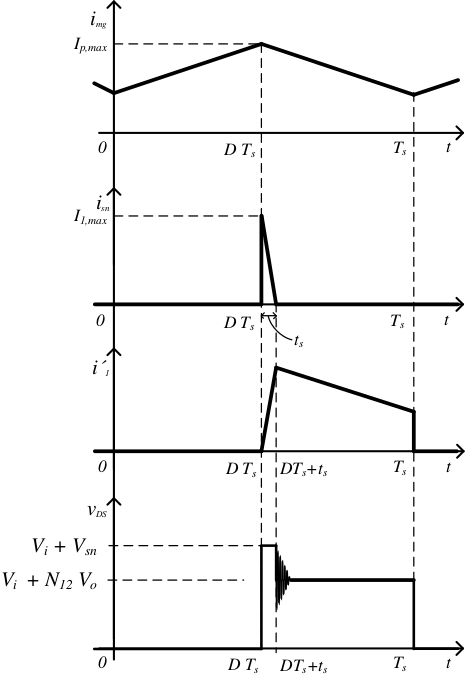
Durante el intervalo \(DT_s < t < DT_s + t_s\), en el que \(t_s\) es el tiempo en el que la corriente que circula por la red snubber se hace 0. En este intervalo, el diodo \(D_{sn}\) conduce. Por tanto, tomando el diodo como ideal, la tensión en el transistor es:
\[ V_{DS} = V_{i} + V_{sn}\]
Haciendo el KVL en la malla que cierra el transformador, la inductancia de dispersión y la red snubber, obtenemos que:
\[ V_1 + V_{L_d} + V_{sn} = 0\]
Si despejamos \(V_{sn}\):
\[V_{sn} = -V_1 – V_{L_d} \]
Por tanto, \(V_{DS}\) queda como:
\[V_{DS} = V_{i} – V_1 – V_{L_d}\]
Como \(V_1 = – \frac{N_1}{N_2}V_o\), \(V_{DS}\) es:
\[V_{DS} = V_{i} + \frac{N_1}{N_2}V_o – V_{L_d}\]
En cuanto a las corrientes, debido a que aparece una tensión en bornes del inductor \(L_{d_1}\), hay una variación de corriente.
\[V_{L_{d_1}} = -V_1 – V_{sn} = \frac{N_1}{N_2} V_o – V_{sn} = L_{d_1} \frac{d i_{L_{d_1}}}{dt} \]
\( \frac{N_1}{N_2} V_o – V_{sn} \) siempre será menor que 0, ya que \(V_{sn} \) será aproximadamente la tensión de ruptura del transistor entre drenador y surtidor.
Por tanto, la corriente es decreciente:
\[ i_{L_{d_1}} = i_{sn}= I_{{mg}_{max}} – \frac{1}{L_{d_1}} \left( V_{sn} – N_{12} V_o \right) \left( t – D T_s\right) \]
La pendiente de la corriente es muy grande, por lo que la corriente se hará 0 en un corto periodo de tiempo. Este periodo es el que habíamos llamado \(t_s\) y es:
\[ t_s = \frac{I_{L_{max}} L_{d_1}}{V_{sn} – N_{12} V_o} \]
Para diseñar la red snubber, se suele elegir una tensión de transistor que sea aproximadamente un 80% de la que el fabricante nos dice que aguanta. Por ejemplo, en el caso de un BUZZ11, la tensión de ruptura es de 50V.
La potencia que disipa la red snubber es igual al producto de la tensión por la corriente. La tensión es \(V_{sn}\) y la corriente sigue la expresión \(i_{sn} = I_{{mg}_{max}} – \frac{1}{L_{d_1}} \left( V_{sn} – N_{12} V_o \right) \left( t – D T_s\right) \).
Por tanto, la potencia instantánea en la red snubber es:
\[ P_{sn} = V_{sn} \left[I_{{mg}_{max}} – \frac{1}{L_{d_1}} \left( V_{sn} – N_{12} V_o \right) \left( t – D T_s\right) \right] \]
Como \(V_{sn}\) se considera constante durante todo este periodo, la potencia tendrá la misma forma de onda que la corriente \(i_{sn}\) pero reescalada por un factor \(V_{sn}\). La potencia media que se disipará en un ciclo completo es:
\[ P_{sn_{AV}} = \frac{1}{T_s} \int{i_{sn}V_{sn} dt} =\frac{ V_{sn}}{T_s}\underbrace{\int{i_{sn} dt} }_{\text{Área del triángulo}} = \frac{ V_{sn}}{T_s} \frac{1}{2} I_{{mg}_{max}} t_s \]
Sabiendo la potencia que se consume y la tensión que se disipa podemos calcular la resistencia simplemente como:
\[ R_{sn} = \frac{V^2_{sn}}{P_{{sn}_{AV}}} \]
Para dimensionar el condensador, lo haremos a partir de la tensión de rizado en el condensador \(C_{sn}\).
El condensador de carga a \(V_{c_{max}}\) y se descarga a través de la resistencia \(R_{sn}\).
La forma de onda de la descarga tendrá un aspecto parecido al siguiente:
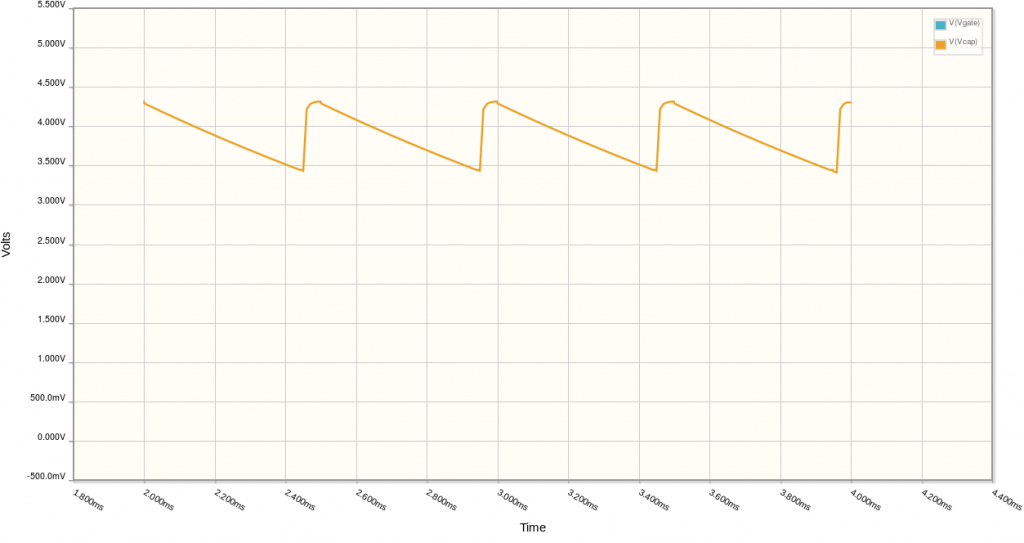 De manera, que si \(R \cdot C \ll T_s\) la descarga es prácticamente lineal.
De manera, que si \(R \cdot C \ll T_s\) la descarga es prácticamente lineal.
La variación de tensión en el condensador es:
\[ \Delta V_{sn} = \frac{V_{sn_{max}} T_s}{R_{sn} C_{sn}} = \frac{V_{sn_{max}} }{R_{sn}C_{sn} f_s} \]
Del que podemos despejar \(C_{sn}\) como:
\[C_{sn} = \frac{V_{sn_{max}} }{R_{sn}\Delta V_{sn} f_s} \]
Un comentario en «Red limitadora de sobretensiones para convertidor Flyback»