Cuando conmutamos a OFF un carga fuertemente inductiva (la cual podemos aproximar como una fuente de corriente) como podría ser el caso de un motor o de un convertidor buck/boost/buck-boost, a causa de la existencia de inductancias parásitas en los cables \(L_d\), aparece una sobretensión debido a la disminución de corriente que pasa por este inductor parásito.
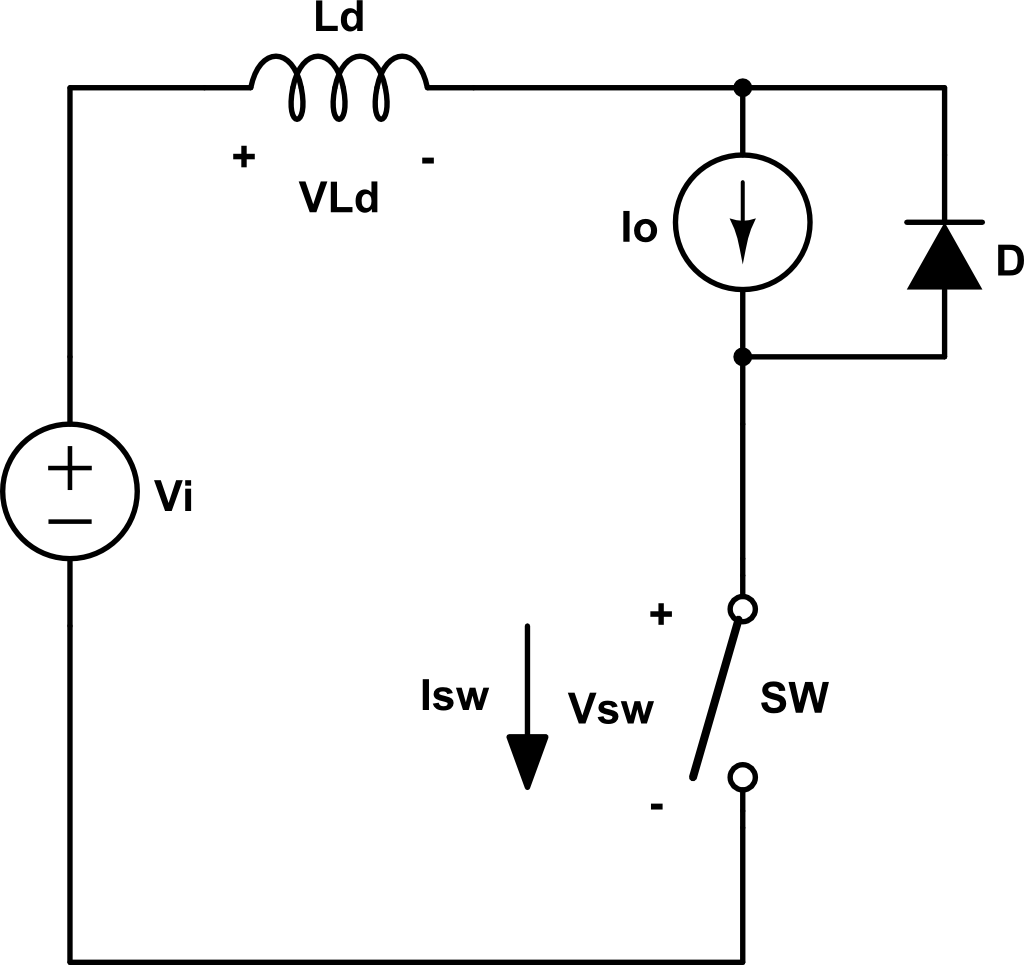
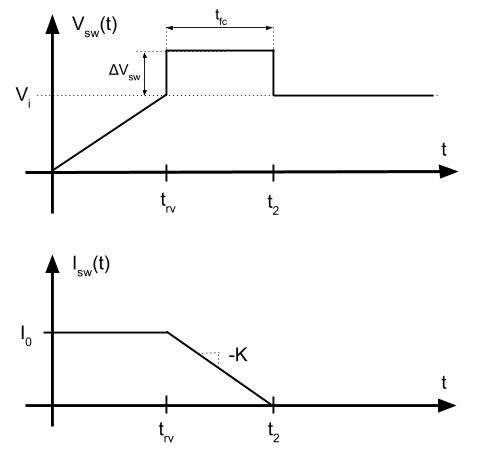
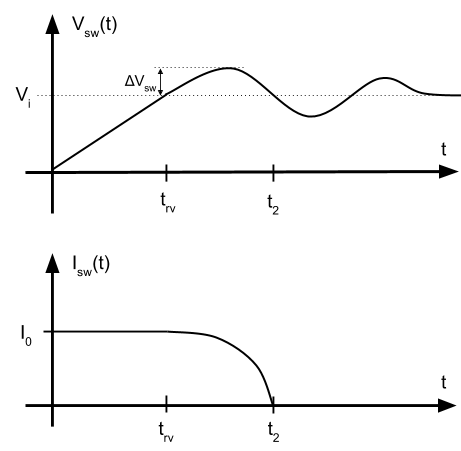
En la conmutación a OFF, la tensión en el switch empieza a subir. Durante el tiempo en el que alcanza el valor de \(V_i\), la corriente que pasa por el interruptor permanece constante.
La tensión \(V_{sw}\) es:
\[ V_{sw} = V_i – V_{L_d} = V_i – L_d \frac{d i_{L_d}}{dt} \]
Una vez la tensión \(V_{sw}\) ha llegado a \(V_i\), instante que llamaremos \(t_{rv}\), la corriente empieza a bajar. La forma de onda es desconocida, pero supondremos que disminuye linealmente con una pendiente K.
\[ i_{L_d} = I_o – K \left( t-t_{rv}\right) \]
El tiempo que tarda en bajar la corriente a 0, la llamaremos \(t_{fc}\). Por tanto, podemos calcular el valor de la pendiente en función del resto de parámetros:
\[ 0 = I_o – K \cdot t_{fc} \]
\[ K = \frac{I_o}{t_{fc}}\]
Por tanto, podemos calcular la tensión en el switch:
\[ V_{sw} = V_i + L_d \frac{I_o}{t_{fc}} \]
En la que podemos identificar la sobretensión como:
\[ \Delta V_{sw} = L_d \frac{I_o}{t_{fc}} \]
Una solución para poder controlar esta sobretensión es el siguiente circuito:
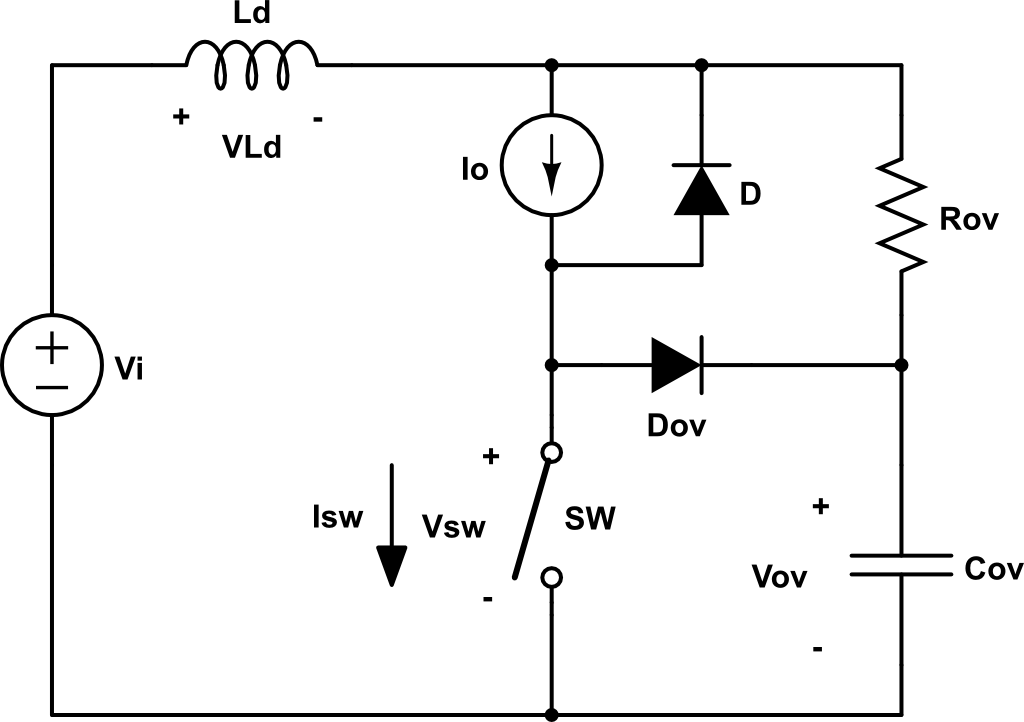
Ahora, cuando la tensión en el switch alcanza \(V_i\), el diodo D y \(D_{ov}\) quedan en circuito abierto (suponiendo que los diodos son ideales).
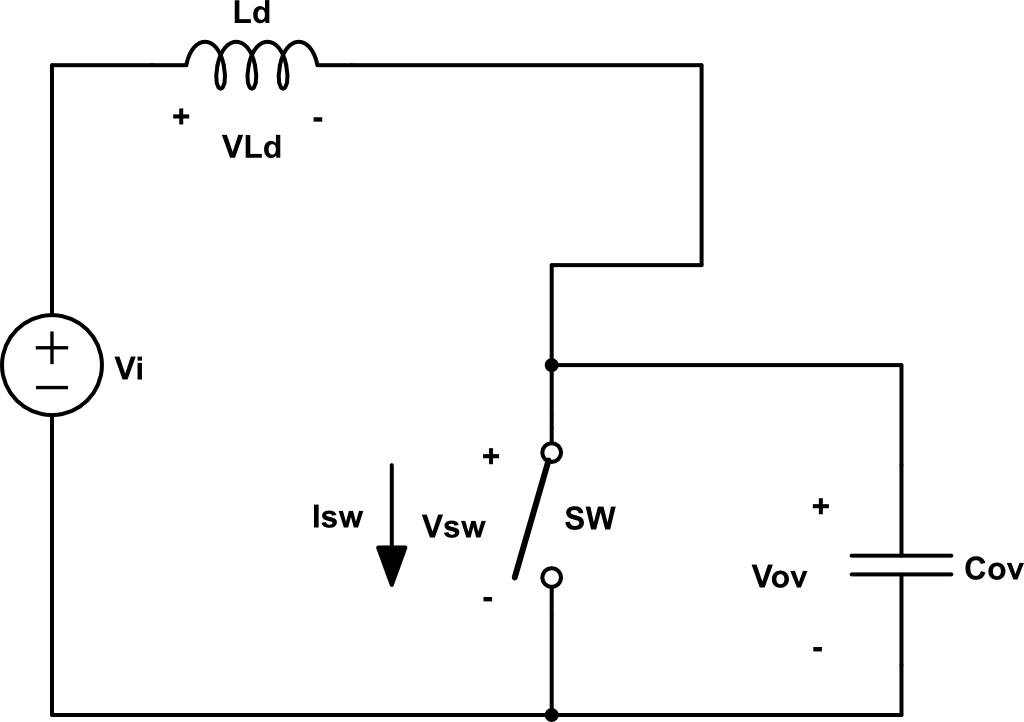
Como tenemos un circuito LC, la corriente oscilará y la podemos aproxima como una forma sinusoidal:
\[ i_{sw} = I_o \cos{\left[\omega \left(t-t_{rv}\right) \right]} \]
Cabe destacar que esta corriente en la realidad estaría amortiguada, de manera que una forma analítica más correcta debería incluir un término \( e^{-\alpha t} \). Sin embargo, para calcular el pico de sobretensión, que es lo que nos interesa, no vale la pena incluir este término.
La tensión en el switch será:
\[ V_{sw} = V_i – V_{L_d} = V_i + L_d \frac{d i_{L_d}}{dt} = V_i + L_d \cdot I_o \cdot \omega \cdot \sin{\left[\omega \left(t-t_{rv}\right) \right]}\]
Donde:
\[ \Delta V_{sw} = L_d I_o \omega = L_d I_o \frac{1}{\sqrt{L_d C_{ov}}} = I_o \sqrt{\frac{L_d}{C_{ov}} }\]
De esta manera, podemos controlar la sobretensión aumentando la capacidad \(C_{ov}\).
En este circuito, cada elemento de la red snubber cumple una función:
- Diodo \(D_{ov}\): se utiliza para conducir cuando nos interesa. Es decir, una vez la tensión en el interruptor ha alcanzado \(V_i\).
- Condensador \(C_{ov}\): se carga a \(V_i\), de manera que cuando el diodo empieza a conducir, limita el cambio brusco de tensión.
- Resistencia \(R_{ov}\): se utiliza para cargar el condensador a \(V_i\). Su valor no es crítico, pero debe permitir la carga del condensador entre \(t_2\) y \(t_3\), que es cuando la sobretensión en el condensador vuelve a \(V_i\).