En el caso de tener una carga inductiva como podría ser el caso de un motor o un convertidor buck/boost/buck-boost con una componente resistiva pequeña, cuyo conjunto podemos aproximar como una fuente de corriente, debido a la inductancia parásita de los cables (\(L_d\)) y de la capacidad parásita del interruptor (\(C_o\)), aparecen una serie de oscilaciones al conmutar a OFF.
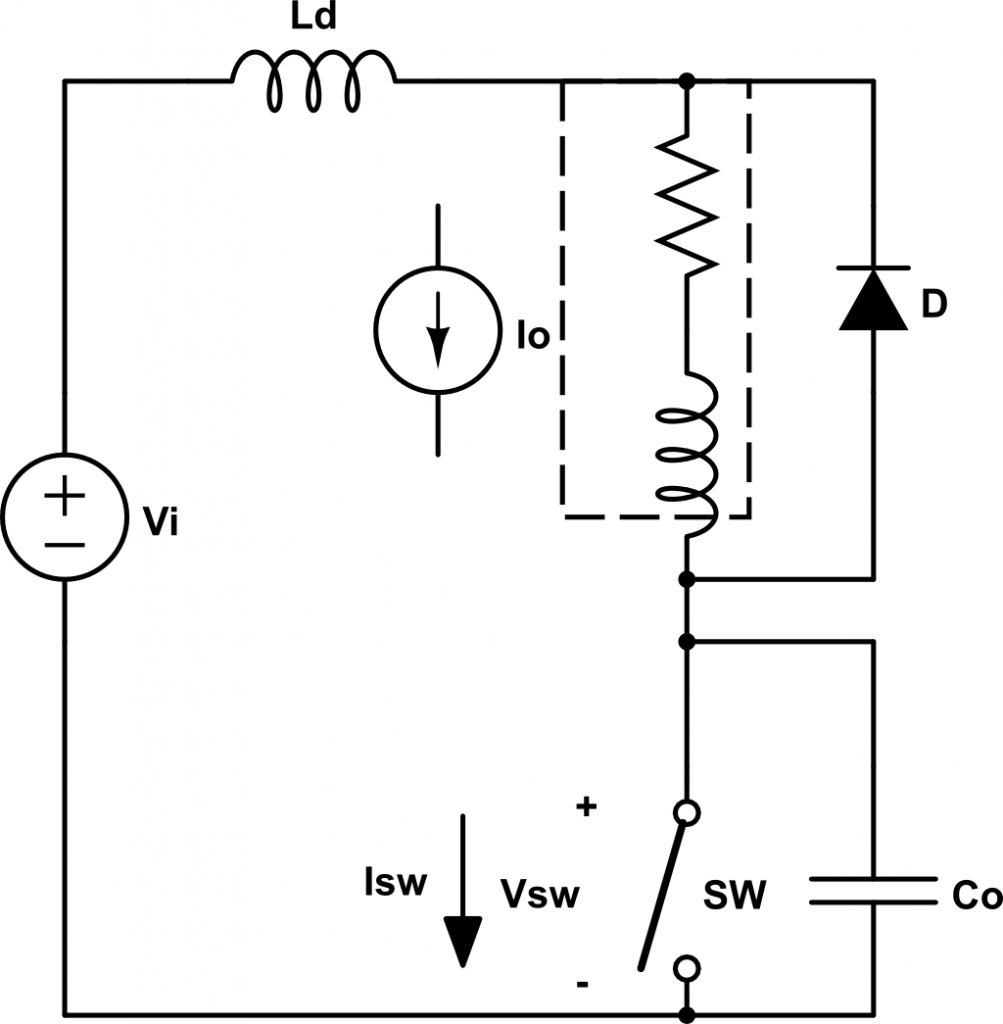
Esto forma un circuito LC que al conmutar crea una oscilación de frecuencia \(f = \frac{1}{2\pi \sqrt{LC}}\).
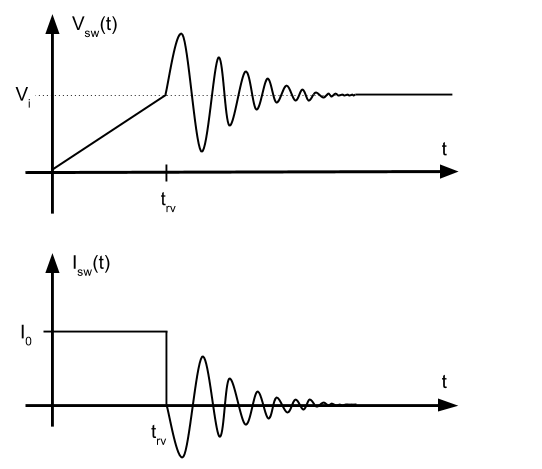
Dependiendo de cómo es el amortiguamiento, obtendremos una forma diferente tanto de la tensión como de la corriente. El tipo de amortiguamiento deseado es el crítico, ya que es el que alcanza el valor final con mayor rapidez.
La red snubber para suprimir oscilaciones consta de una resistencia en serie con un condensador pueste en paralelo con la capacidad parásita del transistor.
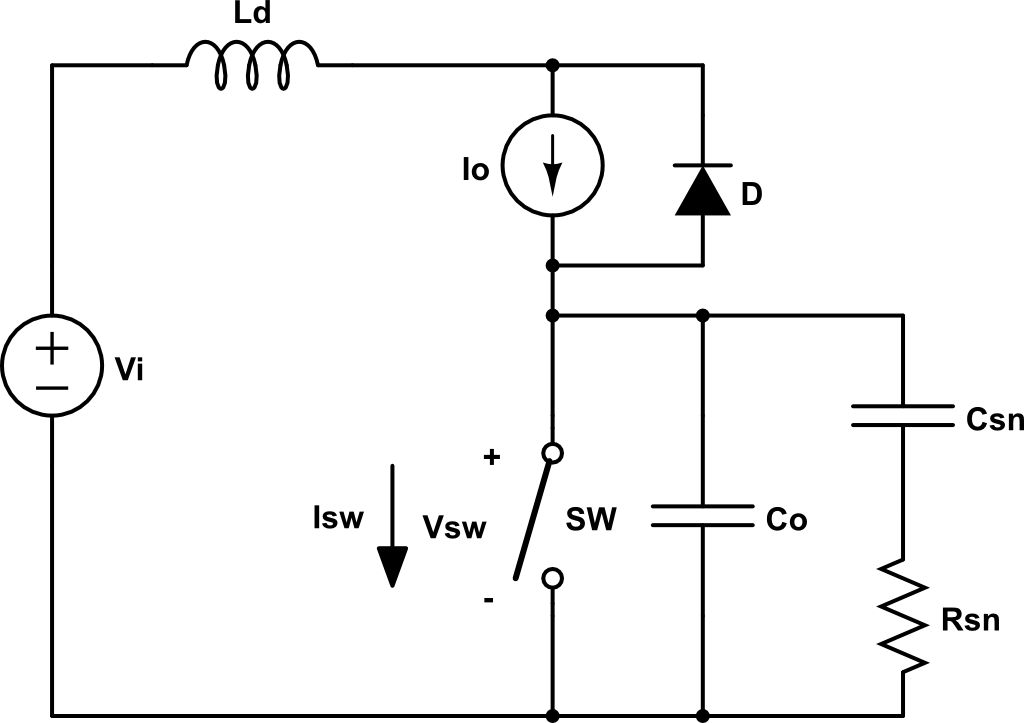
De esta manera, se busca conseguir la oscilación crítica y disminuir la frecuencia de oscilación al añadir más capacidad.
Como no sabemos los valores de inductancia de pérdidas ni la capacidad parásita, añadimos un condensador adicional en paralelo con el transistor con un valor de capacidad que reduzca la frecuencia de oscilación a una fracción de la original. De esta manera:
\[\omega_{sn} = \frac{1}{\sqrt{L_d C_{tot}}}= \frac{\omega_0}{F} = \frac{1}{F\sqrt{L_d C_o}} \]
Donde F es la relación entre la frecuencia de oscilación sin condensador adicional y la frecuencia de oscilación con condensador.
\[ F = \frac{\omega_0}{\omega_{sn}} \]
De aquí encontramos que:
\[C_0 = \frac{C_{sn}}{F^2}\]
Y la inductancia de pérdidas:
\[ L_d = \frac{1}{C_0 \omega_0^2} \]
Para conseguir amortiguamiento crítico, la resistencia que tenemos que poner debe tener el valor:
\[ R_{sn} = F \sqrt{\frac{L_d}{C_{tot}}} \]
Donde \(C_{tot}\) es aproximadamente \(C_o + C_2\). La potencia que se disipará en la resistencia no depende de su valor nominal, si no de la carga del condensador \(C_{sn}\). En un semiperiodo el condensador \(C_{sn}\) se carga a \(\frac{1}{2} C_{sn}V^2_{sw_{off}}\), que es la energía que se descarga en el siguiente semiperiodo. Por tanto, en un ciclo, la variación de energía a través del condensador es:
\[ W_{1~ciclo} = C_{sn}V^2_{sw_{off}} \]
Al estar la resistencia en serie con el condensador, la potencia que se disipa en la resistencia es:
\[ P_{R_{sn}} = \frac{1}{T_s} \int_{1~ciclo}{W~dt} = f_s C_{sn} V_{sw_{off}}^2\]
Las formas de onda resultantes con la amortiguación crítica son ahora:
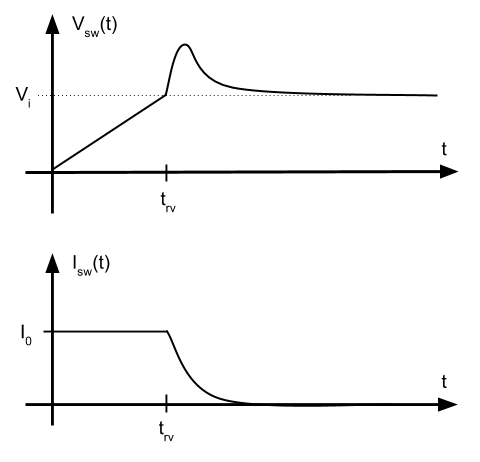
Un comentario en «Red snubber para oscilaciones»