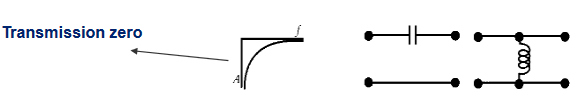Las redes de adaptación son necesarias cuando queremos maximizar la transferencia de potencia entre dos sistemas conectados en cascada. Las redes de adaptación se comportan como filtros en los que en la banda de paso hay adaptación. En la banda de frecuencia a la cual la red no está adaptada, la potencia es reflejada.
Para asegurar la máxima transferencia de potencia, la impedancia de carga debe ser la compleja conjugada del generador.
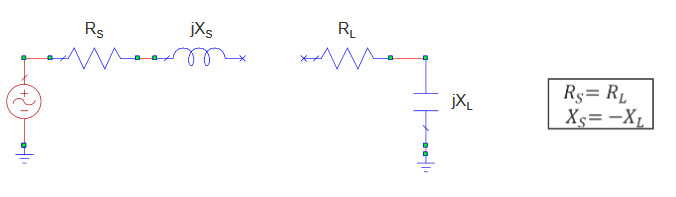
Ceros de transmisión
Dependiendo de la disposición de inductores y condensadores, es posible crear ceros de transmisión en los cuales no haya transferencia de señal entre la entrada y la salida.
Cero de transmisión en DC ( \(f= 0\) ).
Para conseguir un cero de transmisión en DC podemos poner un condensador en serie entre entrada y salida o una inductancia en derivación (en paralelo a masa).
La pendiente con la que tiende a 0 el diagrama de Bode es de -20 dB/dec o 6 dB/oct.
Para calcular las octavas que hay entre dos frecuencias:
\[N_{octavas} = \log_2{\frac{f_{sup}}{f_{inf}}}\]
Para calcular el número de décadas entre dos frecuencias:
\[N_{dec} = \log_{10}{\frac{f_{sup}}{f_{inf}}}\]
Para pasar de décadas a octavas:
\[N_{dec} = 0.3 N_{octavas}\]
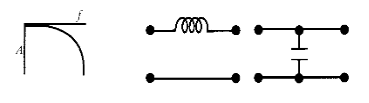
Cero de transmisión en \(f=\infty\)
Para conseguir un cero de transmisión a frecuencias muy altas, hay que poner un inductor en serie o un condensador en derivación.
La pendiente en el diagrama de Bode es de 20 dB/dec o 6 dB/oct.
Cero a \(0< f_R < \infty\)
Para crear un cero a una frecuencia que no es ni DC ni a frecuencias infinitas, es necesario utilizar circuitos resonadores (también llamados circuitos tanque).
Existen dos tipos de resonadores: los serie y los paralelo.
Los resonadores serie constan de un condensador y un inductor en serie que a la frecuencia de resonancia equivalen a un cortocircuito. Por tanto, para forzar un cero de transmisión, será necesario poner un resonador serie en derivación.
Por otra parte, tenemos los resonadores paralelo, que a la frecuencia de resonancia son equivalentes a un circuito abierto. Para crear un cero de transmisión basta con ponerlos en serie entre la entrada y la salida del circuito.
La frecuencia de resonancia de un resonador es: \(f_R = \frac{1}{2\pi\sqrt{LC}}\)
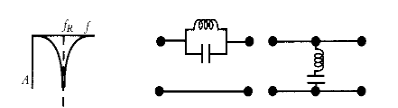Topologías de adaptación con elementos concentrados
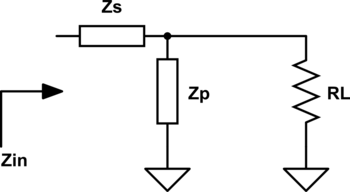
Existen 3 topologías de redes en las que se necesita una red de adaptación para conseguir MTP:
- \(R_s = R_L\)
- \(R_s \neq R_L\)
- La impedancia de carga o fuente es compleja.
1) Impedancia compleja con \(R_S = R_L\)
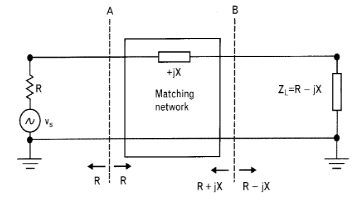En esta red de adaptación el valor de la parte real de la impedancia coincide con la impedancia del generador. Sin embargo, hay un parte imaginaria que es necesario eliminar. En este caso es tan sencillo como añadir en serie una impedancia imaginaria de signo contrario. Es decir, si la reactancia es positiva (carácter inductivo), habrá que poner un condesador. Si la reactancia es negativa (carácter capacitivo), habrá que poner un inductor. De esta manera, es equivalente a tener un circuito tanque en serie. Sin embargo, como ya hemos visto anteriormente esta solución solo es válida para una frecuencia ya que ambos valores solo se anulan a su frecuencia de resonancia.
Una manera de medir cómo de estrecha será la banda a la cual se da la adaptación es utilizando el factor de calidad Q. En circuitos paso banda, el factor de calidad establece la relación que hay entre la frecuencia de paso y el ancho de banda a -3 dB. Es decir:
\[Q = \frac{f_0}{BW}\]
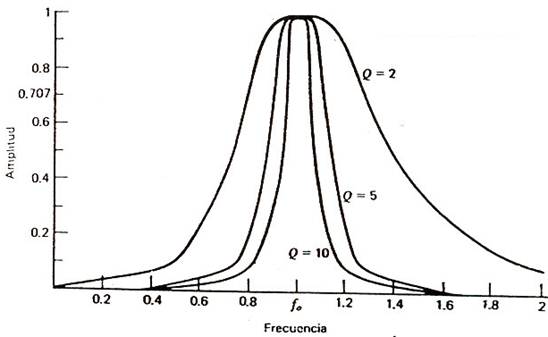Como vemos, si el ancho de banda es grande (poco selectivo), la Q es pequeña. Si el filtro es muy selectivo, la Q es grande.
Este parámetro puede ser medido en función de la reactancia y el valor de la resistencia de carga:
\[Q = \frac{X_L}{2R}\]
Por tanto, si la resistencia es grande la Q es pequeña (el filtro es poco selectivo) y la banda de adaptación es ancha. Si por el contrario la resistencia es pequeña lleva a Q muy grandes (muy selectivo). Ambos extremos son difíciles de solucionar en la práctica, ya que conseguir un filtro muy selectivo o de gran ancho de banda es complicado.
2) Impedancia compleja con \(R_S \neq R_L\)
En este caso, las resistencia de carga y de fuente no coinciden. Es por ello que se necesita subir o bajor el valor de la resistencia de carga para adaptar con la impedancia de fuente.
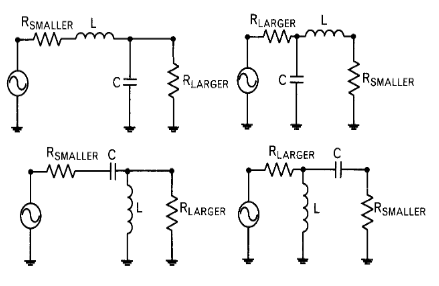
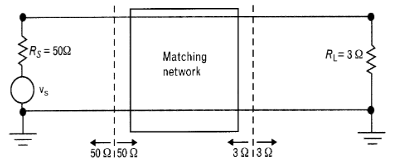Para diseñar este tipo de redes de adaptación se utilizan redes en L:
Sin embargo el principal problema del diseño de este tipo de redes es que su cálculo es muy largo sobretodo cuando el número de elementos aumenta.
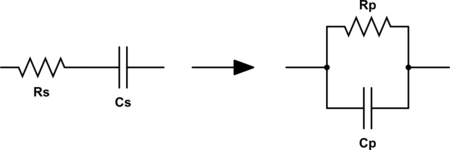
Este proceso se puede simplificar si utilizamos equivalencias serie-paralelo de circuitos RC y RL.
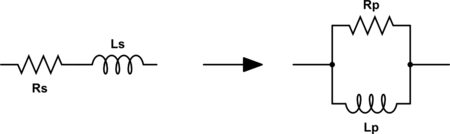
\[Q_s = \frac{X_s}{R_s} = Q_p = \frac{R_p}{X_p} = Q\]
\[R_p = \left( 1 + Q^2 \right)R_s\]
\[C_p \approx C_s\]
\[L_p \approx L_s\]
El factor de calidad (Q) indica cómo de ideal es un dispositivo a la hora de almacenar energía. Un dispositivo que pueda almacenar toda la energía sin disiparla tendrá un factor de calidad que tenderá a infinito. Una manera fácil de saber cómo es la expresión del factor de calidad con una resistencia en serie es pensando que si la resistencia en serie es muy grande, esta disipará mucha potencia y el factor de calidad será bajo. Por tanto, en la expresión del factor de calidad para un dispositivo con una resistencia en serie, el valor de la resistencia está en el denominador \(Q_p = \frac{R_p}{X_p}\)
La manera en la que se deben colocar los elementos es la siguiente: con la resistencia de mayor valor, un elemento en paralelo (para bajar su impendancia). Y con la resistencia de menor valor un elemento en serie (para subir su impedancia).
Para calcular los valores de los elementos hay que igualar el factor de calidad Q de las redes serie y paralelo:
\[Q_s = Q_p = \sqrt{\frac{R}{r} – 1}\]
donde R es la resistencia con el valor nominal más alto y r la resistencia más baja.
Una vez calculado el factor de calidad, se obtiene el valor de la reactancia y con ello, el valor nominal del condensador o inductor.
Existen 4 disposiciones distintas:
Ejemplo:
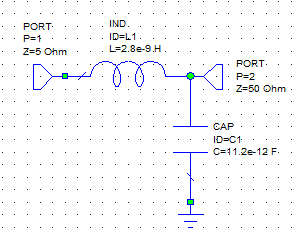
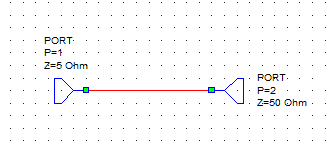Queremos adaptar estos dos puertos para que a la frecuencia de 850 MHz haya MTP y al mismo tiempo que la polarización en DC también pueda pasar del puerto 1 al 2.
Debido a que no podemos bloquear la continua, no podemos utilizar un condensador en serie con la resistencia del puerto 1. Por tanto, tenemos que utilizar la red en L con una bobina en serie y un condensador en derivación:
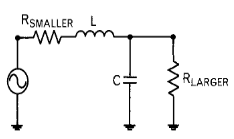Para calcular los valores de L y C:
\[Q_s = Q_p = \sqrt{\frac{R}{r} -1 } = \sqrt{\frac{50}{5} -1} = 3\]
\[Q_s = \frac{X_s}{R_s} \Rightarrow X_s = Q \cdot R_s = 2\pi f L\]
\[L = \frac{Q \cdot R_s}{2\pi f} = \frac{3 \cdot 5}{2\pi \cdot 850\cdot 10^6} = 2.8\text{ nH}\]
\[Q_p = \frac{R_p}{X_p} \Rightarrow X_p = \frac{R_p}{Q_p} = \frac{1}{2\pi f C}\]
\[C = \frac{Q_p}{2\pi f R_p} = 11.2\text{ pF}\]
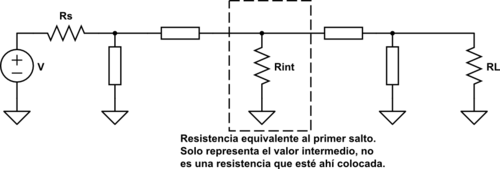
Sin embargo, cuando la diferencia de resistencias es muy grande, es posible que necesitemos unos valores de Q que no nos convengan en la práctica (recordar que \(Q = \sqrt{\frac{R}{r} – 1}\) ).
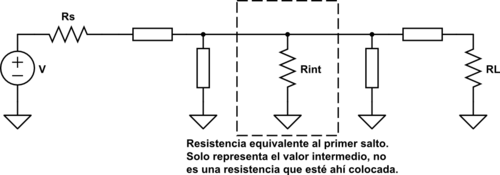
Podemos hacer varios saltos de impedancia en lugar de uno solo. Esto da lugar a las redes en T y redes en π:
Por tanto disponemos de 3 tipos de redes: las redes en L, las redes en T y las redes en π. Con estas redes en T y π podemos aumentar el ancho de banda ya que al hacer saltos más pequeños de impedancia, la Q disminuye y el ancho de banda aumenta. Con las redes en L podemos disminuir el ancho de banda, ya que la resistencia virtual está entre un valor de \(R_{int} < r\) o \(R_{int} > R\).
Aumento del ancho de banda
Para aumentar el ancho de banda hay que utilizar una red en T o π. Si queremos una red de adaptación con un ancho de banda grande, la Q deberá se baja. Para que la Q sea baja, los saltos de impedancia deben de ser pequeños. Por tanto, podemos hacer saltos intermedios que tengan una Q menor y de esta manera aumentar el ancho de banda:
Para que una red en T o en π dé un ancho de banda mayor, el valor de la resistencia \(R_L\). Un valor adecuado es el que da la media geométrica entre los dos valores:
\[R_{int} = \sqrt{R_s R_L}\]
Por tanto, las redes en T y en π no sirven para adaptar resistencias de carga y generador ya iguales ya que se hacen saltos de impedancia.
Si queremos poner \(m\) sería:
\[R_m = R_S^{\frac{n-m}{n}} R_L^\frac{m}{n}\]
Reducción del ancho de banda
Para reducir el ancho de banda debemos hacer saltos de impedancia más grandes. Esto se puede conseguir de la siguiente manera:
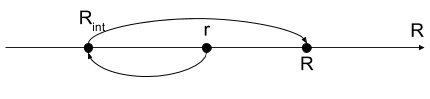El valor de \(R_{int} > R\). Ambas combinaciones harán que el ancho de banda sea menor.
3) Impedancias complejas
Una tercera forma de adaptar las impedancias de carga y fuente es mediante absorción o resonancia de la parte compleja de impedancia. Estas soluciones son de banda muy estrecha.
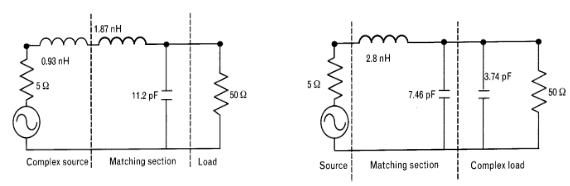La absorción consiste en utilizar la parte compleja de la carga o fuente como parte de la red de adaptación. Es decir, si necesitamos un condensador de 10 pF y la carga tiene un condesandor equivalente de 5 pF, solo será necesario poner un condensador de 5 pF ya que los otros 5 pF restantes los pondrá la parte imaginaria de la impedancia de carga.
La otra estrategia es hacer resonar la reactancia de la carga para poder eliminarla a la frecuencia de trabajo. Es decir, si tenemos un condensador en derivación, podemos ponerle un inductor en paralelo para que resuene a la frecuencia de trabajo y haya máxima transferencia de potencia.
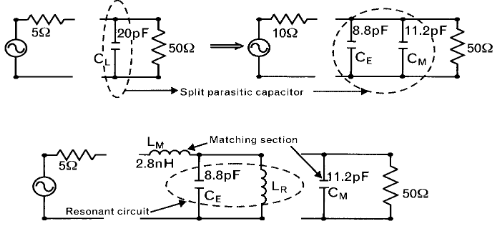
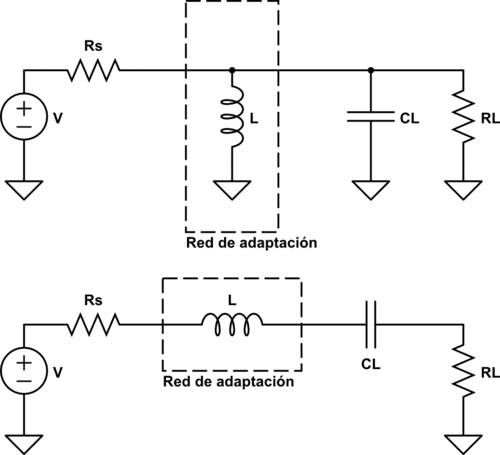También podemos resonar solo una parte de la reactancia y utilizar la otra para conformar la red de adaptación en L:
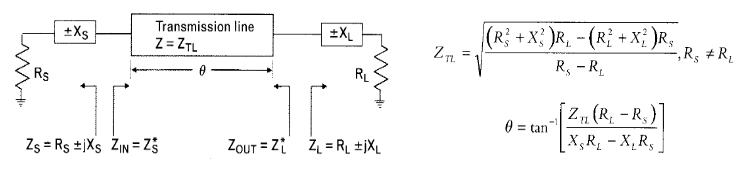
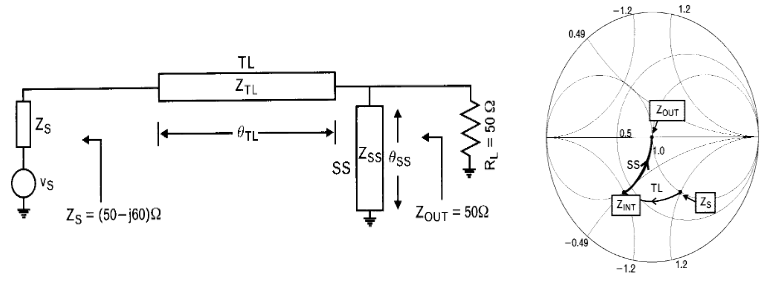
Adaptación con líneas de transmisión
En las líneas de transmisión tenemos 2 grados de libertad: la impedancia característica y la longitud eléctrica. Jugando con estos valores podemos sintetizar valores de inductancia y capacitancia utilizando transformadores en \(\frac{\lambda}{4}\) y stubs en paralelo. Sin embargo, las líneas de transmisión no sirven para adaptar los casos en los los valores de resistencia de carga y fuente sean diferentes.
