Los transformadores son elementos muy útiles cuando es necesario modificar la impedancia vista desde un punto del circuito. Cuando estamos diseñando un filtro paso banda y queremos conectar la siguiente etapa es muy importante no modificar la resistencia del circuito, ya que modificaríamos su ancho de banda. Por otra parte, construir transformadores es algo caro, que ocupa mucho espacio y poco práctico. Por ello intentar buscar una solución sin que utilice bobinas es una buena idea.
Transformación paralelo-serie
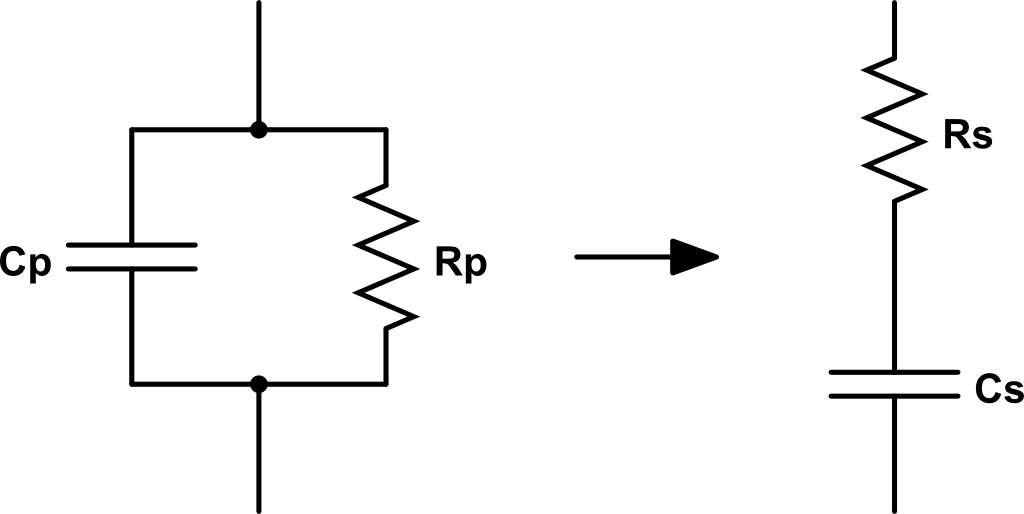
Para empezar, deberemos saber como pasar del paralelo de una resistencia y un condensador a la disposición en serie de una resistencia y un condensador:
La impedancia equivalente del paralelo es:
\[Z = \frac{R_p}{1 + R_p C_p j \omega} = \frac{R_p}{1+R_p C_p j \omega} \cdot \frac{1-j\omega R_p C_p}{1-j\omega R_p C_p}=\frac{R_p(1-j\omega R_p C_p)}{1+\omega^2 R_p^2 C_p^2}=\frac{R_p}{1+\omega^2 R_p^2 C_p^2} – \frac{j\omega R_p^2 C_p}{1+\omega^2 R_p^2 C_p^2}\]
Si \(R_p >> \frac{1}{C_p\omega}\), entonces podemos aproximar la impedancia equivalente como:
\[Z \approx \frac{1}{R_p C_p^2 \omega^2}-j\frac{1}{\omega\cdot C_p}\]
Por tanto:
\[R_s = \frac{1}{R_p C_p^2 \omega^2}\]
\[C_s = C_p\]
Como hemos visto esto solo es válido cuando la impedancia de la resistencia paralela es mucho mayor que la impendancia del condensador. Por tanto, podemos reescribir la condición como \[f >> \frac{1}{2\pi R_p C_p}\]
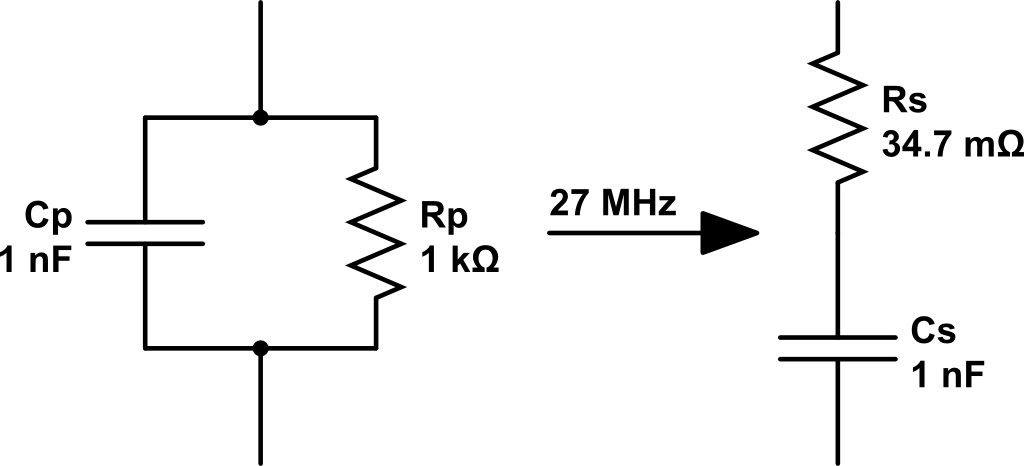
Veamos un ejemplo:
Primero tenemos que comprobar que a la frecuencia de trabajo (27 MHz) se cumplen la condición necesaria para que la aproximación sea válida:
\[f >> \frac{1}{2\pi R_p C_p} = \frac{1}{2\pi 1k\Omega 1nF}=159 kHz\]
Como vemos, a 27 MHz cumplimos de sobra la condición. Para calcular \[C_s\]:
\[R_s = \frac{1}{R_p C_p^2 \omega^2} = \frac{1}{1 k\Omega (1nF)^2 (2\pi\cdot 27 MHz)^2}=0.0347 \Omega\]
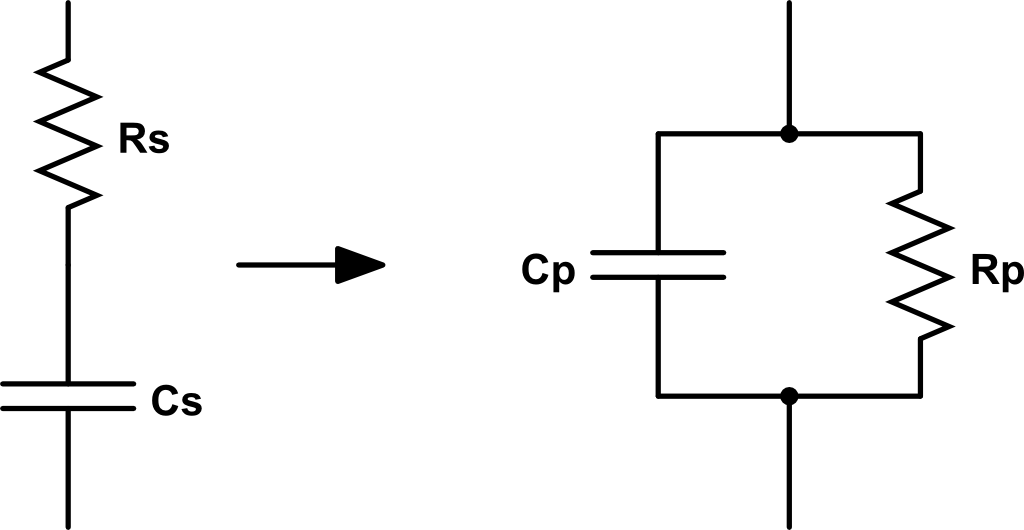
Transformación serie-paralelo
De la misma manera, podemos transformar el circuito serie en paralelo.
Ahora las identidades son:
\[R_p = \frac{1}{R_s C_s^2 \omega^2}\]
\[C_p = C_s\]
Siempre y cuando \[f >> \frac{1}{2\pi R_p C_p}\]
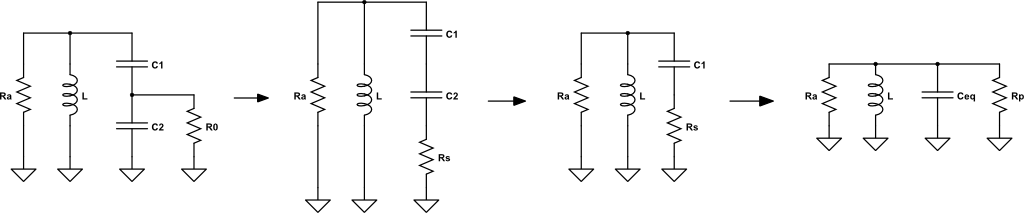
Uso como transfomador
Como vemos, de esta manera conseguimos tener un condensador y una resistencia en paralelo del valor:
\[C_{eq}=\frac{C_1\cdot C_2}{C_1 + C_2}\]
\[R_p = R_0 (1+\frac{C_2}{C_1})^2\]
Como vemos \((1+\frac{C_2}{C_1})^2\) veces más grande.