maxdB = max(meanFrequency);
maxPos = find(meanFrequency == maxdB);Mes: febrero 2017
Para generar señales digitales periódicas, como por ejemplo senos o cosenos, se suele utiliza la técnica de síntesis digital directa. Esta consiste en almacenar la señal en una memoria y recorrer las diferentes direcciones de la memoria para obtener la señal. Por tanto, se necesita de un contador que incremente un determinado número de pasos la dirección de memoria a la que hay que acceder.

La frecuencia sintetizada depende de 3 factores:
- P: el incremento que se hace de la dirección de memoria
- \(f_{clk}\): la frecuencia de reloj
- \(2^M\): el número de muestras que hay de un periodo de la señal.
Ejemplo: síntesis de un seno de 1 Hz
Tenemos almacenado en un memoria el ciclo completo de un seno como aparece en la imagen utilizando 16 muestras (\(2^M = 16\)) :
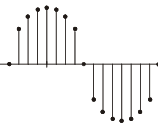 La frecuencia del reloj es de 8 Hz, es decir, saca 8 muestras por segundo. Por tanto, para obtener una frecuencia del seno de salida de 1 Hz, debemos sacar 8 muestras. Esto conduce a la conclusión de que debemos obtener las muestras de la memoria de 2 en 2. Lo que significa que P = 2.
La frecuencia del reloj es de 8 Hz, es decir, saca 8 muestras por segundo. Por tanto, para obtener una frecuencia del seno de salida de 1 Hz, debemos sacar 8 muestras. Esto conduce a la conclusión de que debemos obtener las muestras de la memoria de 2 en 2. Lo que significa que P = 2.
Por tanto,
\[ f_{sintetizada} = \frac{P f_{clk}}{2^M} \]
El máximo paso que se puede dar es \(P = 2^{M-1}\) para poder cumplir el teorema de Nyquist y tener una señal parecida a la de la imagen:

En este caso, la frecuencia es máxima y corresponde a \(\frac{f_{clk}}{2}\). El mínimo paso que se puede dar es P= 1, en el que la frecuencia es mínima y corresponde a \(\frac{f_{clk}}{2^M}\).