STDP = Servicios de Telecomunicaciones de Telefonía Disponible al Público
TBA = Telecomunicaciones de Banda Ancha
STDP = Servicios de Telecomunicaciones de Telefonía Disponible al Público
TBA = Telecomunicaciones de Banda Ancha
Tasa de transmisión: 14 Mb/s
Ancho de banda: 5 MHz
\(\left.P_{Tx}\right|_{EB} = 43~dBm\)
Factor de ruido del receptor: \(\left.F\right|_{Rx} = 4~dB\)
Frecuencia de la portadora \(f_c = 900~MHz\)
Ganancia del transmisor: \(G_{Tx} = 15~dB\)
Ganancia del terminal de usuario: \(G_{UE} = 0~dB\)
Modelo a utilizar:
– \(f_c = 900~MHz\)
– Altura de la antena transmisora: \(h_{EB} = 15~m\) sobre edificios
\[B = 5 MHz\]
| Ancho de banda nominal (MHz) | 1.4 | 3 | 5 | 10 | 15 | 20 |
| Ancho de banda ocupado (MHz) | 1.08 | 2.7 | 4.5 | 9 | 13.5 | 18 |
| Número de RB (UL o DL) | 6 | 15 | 25 | 50 | 75 | 100 |
| Número de subportadoras | 72 | 180 | 300 | 600 | 900 | 1200 |
\[B = 5 MHz \rightarrow Tabla \rightarrow N_{RB} = 25\]
\[L_{prop} = 120.9 + 37.6 \log{R}~[km]\]
De las pérdidas de propagación también podemos extraer el parámetro \(\gamma\) ya que \(10\gamma\) es el número que multiplica el término \(\log{R}\).
\(\gamma = 3.76\)
\[\eta = throughput = \frac{14~Mb/s}{5~MHz} = 2.8~b/s/Hz\]
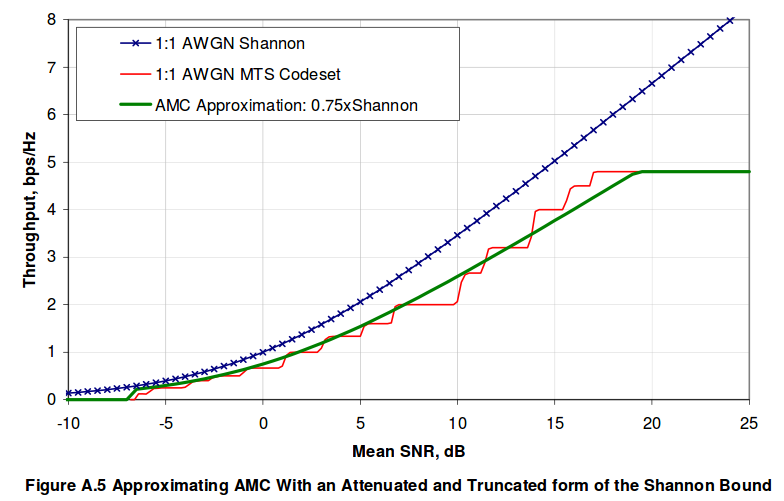
De la gráfica podemos ver que la SINR(dB) equivalente es aproximadamente 11 dB. También podemos sacarlo de la fórmula del límite de Shannon corregida \(\eta = \frac{C}{B} = 0.75 \log_2{(1+SNR)}\)
\[SINR(dB) = 11dB\]
\[SINR(dB) < CINR(dB)\]
\[\left.CIR(dB)\right|_{sectorización} = 10\log{ \left[3 \cdot \frac{1}{6} \left( \frac{D}{R} \right)^\gamma\right]} = 10\log{ \left(\frac{1}{2} q^\gamma\right)}\]
¿Qué k es válido?
\[k = 1 \rightarrow CIR=5.96~dB\]
\[k = 3 \rightarrow CIR=14.96~dB\]
\[k = 4 \rightarrow CIR=17.27~dB\]
Por tanto \(k = 3\), ya que el mínimo k optimiza el despliegue (es más barato).
\[L_{total} (dB) = 121.5 + \left.10\log{\left( 1 – \frac{10^{\frac{11~dB}{10}}}{10^\frac{14.92~dB}{10}} \right)}\right|_{k=3} + 43~dBm – 4~dBm – 10 \log{25} – 11~dB = 133.26~dB\]
\[L_{prop} (dB) = L_{total} (dB) + G_{Tx}(dB) + G_{UE}(dB) = 133.26 + 15~dB + 0~dB = 148.26~dB\]
\[L_{prop} (dB) = 120.9 + 37.6 \log{R} = 148.26~dB\]
\[\log{R} = \frac{148.26-120.9}{37.6} \Rightarrow R = 10^{\frac{148.26-120.9}{37.6}} \approx 5.34~km\]
\(P_{util} = P_u\),\( P_{interfencia} = P_i\) y \(P_{noise} = P_n\)
\[SINR = \frac{P_u}{P_i + P_n} \Rightarrow SINR < \frac{P_u}{P_i} = CIR\]
\[\frac{1}{SINR} = \frac{P_i}{P_u}+\frac{P_n}{P_u} = \frac{1}{CIR} + \frac{1}{CNR}\]
\[\frac{1}{CNR} = \frac{1}{SINR} \left( 1- \frac{SINR}{CIR} \right)~~~\left(1\right)\]
De aquí podemos expresar la CNR como:
\[CNR = SINR \left( \frac{1}{1-\frac{SINR}{CIR}} \right)\]
Que pasado a dBs:
\[CNR(dB) = SINR(dB) – 10\log{\left(1-\frac{SINR}{CIR} \right)}\]
\[\left.P_u\right|_{Rx} = \frac{P_{Tx}}{l_{total}}~~~\left(2\right)\]
\[l_{total} = \frac{l_{prop} \cdot l_{conectores} \cdot l_{cables} \cdot l_{penetración~edificios}}{g_{antenas}}\]
De (1) y (2):
\[L_{total}(dB) = \left.P_{Tx}\right|_{EB} (dBm) – \left.P_{u}\right|_{Rx} (dBm)~~~ \left(3\right)\]
Aprovechando la definición de CNR:
\[\left.CNR\right|_{Rx} (dB) = \left.P_{u}\right|_{Rx} (dBm) – P_{n}(dBm)\]
\[\left.P_{u}\right|_{Rx} (dBm) = \left.CNR\right|_{Rx} (dB) + P_{n}(dBm)\]
\[\left.P_{u}\right|_{Rx} (dBm) = SINR(dB) – 10\log{\left(1-\frac{SINR}{CIR} \right)} + P_{n}(dBm)\]
Sustituyendo ahora en (3):
\[L_{total}(dB) = \left.P_{Tx}\right|_{EB} (dBm) – SINR(dB) + 10\log{\left(1-\frac{SINR}{CIR} \right)} – P_{n}(dBm)\]
La potencia del ruido es:
\[\left.P_n~(dBm)\right|_{LTE} = 10 \log{(k T_0 B F)} + 30~dB\]
donde \(B=180~kHz \cdot N_{RB}\) (180 kHz = 15 · 12)
\[\left.P_n~(dBm)\right|_{LTE} = 10 \log{(k T_0 12 \cdot 15~kHz)} + 30~dB + F(dB) + 10\log{(N_{RB})}\]
\[\left.L_{total}(dB)\right|_{LTE} = 121.5 + 10\log{\left(1-\frac{SINR}{CIR} \right)} + P_{Tx}(dBm) – \left.F\right|_{Rx}(dB) – 10 \log{N_{RB}} – SINR(dB)\]
De esta manera podemos calcular las pérdidas totales, que por otra parte, sabemos que:
\[\left.L_{total}(dB)\right|_{LTE} = L_{prop} (dB) + L_{conectores}(dB) + L_{cables}(dB) + L_{penetración}(dB) – \left.G\right|_{EB} (dB) – \left.G\right|_{Mobile~Station} (dB)\]