- Por debajo de 70 ºC no hay apenas cambios en la vida útil de un componente, como norma general (puede haber componentes específicos que sí).
- Un test en una cámara climática no siempre es fiable debido al funcionamiento de la cámara. Se crea una circulación de aire caliente para calentar toda la cámara, pero esto puede hacer que el circuito se esté refrigerando por convección forzada. Por tanto, una vez alcanzada la temperatura deseada habría que parar el ventilador y comprobar que la temperatura del circuito no aumenta.
- Un disipador (heat-sink) de la misma área que el integrado que se quiere refrigerar no servirá de nada. De hecho, empeorará la refrigeración del componente al añadir una resistencia térmica adicional entre el encapsulado y el aire.
- Reducir la temperatura media de los componentes de un circuito no es una buena estrategia. Solo el 5% de los componentes de un circuito suele disipar calor, por lo que hay que concentrarse en bajar la temperatura de aquellos que realmente disipan. Un buen diseño tiende a disminuir la temperatura de ese 5% y a aumentar la del 95% restante.
- En las especificaciones de un ventilador se muestra el volumen de aire que es capaz de mover por minuto, normalmente expresado en CFM (cubic feet per minute, pies cúbicos por minuto). Sin embargo, hay que tener en cuenta la resistencia que ofrece aquello que se ponga delante del ventilador ya que esto hará que el flujo efectivo sea mucho menor. Dimensionar con un factor 2 para evitar problemas.
- Uno de los parámetros que dan los fabricantes es la resistencia térmica entre el silicio y el encapsulado \(R_{ja}\) ó \(\Theta_{jc}\). Sin embargo no es el parámetro más importante a la hora de realizar el diseño térmico del circuito, ya que otros factores como la posición de otros componentes que disipan calor o el área de PCB y cobre debajo del componente pueden tener mucha relevancia a la hora de determinar la temperatura del componente.
- Los disipadores tipo pin fin no son siempre mejores que los de extrusión. Cada uno tiene un propósito y se tiene que tener en cuenta a la hora de elegirlo. Por ejemplo, la dirección del aire si se utiliza un ventilador o la dirección ascendente del aire caliente.
- Para medir la temperatura de un componente deben pasar horas o incluso días para determinar de manera correcta su temperatura.
- El mejor diseño térmico es muy posible que sea el peor desde el punto de vista electrónico.
La temperatura ambiente máxima para la mayoría de dispositivos comerciales es de 70 ºC. En superficies metálicas, a partir de 60 ºC se producen ampollas en los dedos. Para el plástico o madera es a partir de 70-80 ºC. La temperatura de transición vítrea del FR4 es de 105-130 ºC por lo que puede comenzar a deformarse a partir de esta temperatura.
Es muy importante definir al principio del proyecto los objetivos térmicos del circuito para tenerlos presentes a lo largo de todo el proceso de diseño.
Refrigeración por conducción
Ecuación de conducción:
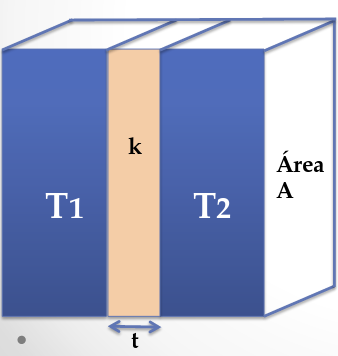
\[ \Delta_T = T_1 – T_2 = \frac{P\cdot t}{k\cdot A} \]
Y la resistencia térmica es:
\[ R = \frac{t}{k\cdot A}\]
Donde k es la conducción térmica (ºC/m·K), t es el grosor (thickness), \(T_x\) es la temperatura entre ambas interfaces y R la resistencia térmica en ºC/W.
En una PCB el que realmente conduce el calor es el cobre, no el FR4 ya que la conductividad térmica del FR4 es de 0.25 W/m·K (10 veces mejor conductor que el aire) mientras que la del cobre es de 360 W/m·K (1200 mejor conductor que el FR4).
En la conducción longitudinal o lateral del cobre, la resistencia del cobre de 1 oz de grosor (35 \(\mu m\)) es de 80 ºC/W. Para el FR4 de 1.6 mm es de 2500 ºC/W. Por tanto, la diferencia térmica entre el FR4 y el cobre es muy grande, siendo el FR4 un aislante térmico en comparación y se puede decir que todo el calor lateral o longitudinal es conducido por el cobre.
La conducción transversal (de cara top a bottom) de una PCB es buena. El cobre tiene muy poca resistencia y un FR4 de grosor 1.6 mm, tiene una resistencia de 64 ºC/W. El efecto del soldermask es despreciable frente a la resistencia del FR4, por lo que no vale la pena dejar areas de cobre descubierto para mejorar la disipación.
La resistencia térmica de una PCB en la dirección transversal (de cara top a bottom) es aproximadamente 60 ºC/W y una vía es aproximadamente 40 ºC/W, por lo que colocar varias vías térmicas en paralelo puede ser una buena solución para disminuir la resistencia térmica.
Refrigeración por radiación
En la refrigeración por radiación, hay que tener en cuenta la emisividad del material, el área de la superficie radiante, la temperatura del material y la temperatura de su entorno así como el ángulo sólido con el que la superficie ve algo más frío que ella.
Los metales pulidos radian menos que los rugosos, por eso el MacBook Pro es aluminio rugoso.
\[ P = \epsilon A_s \sigma \left(T_s^4 – T_{ent}^4 \right) f_v \]
Los plásticos opacos y la madera presentan valores altos de emisividad.
Refrigeración por convección natural
En la refrigeración por convección natural, hay que tener en cuenta el coeficiente de convección, el área, la temperatura de la superficie del objeto y la temperatura del fluido.
El coeficiente de convección \(h_{conv}\) depende de la longitud del cuerpo caliente a lo largo de la dirección de convección, de la presión atmosférica y de la diferencia de temperatura entre superficie y ambiente. Y un hecho muy significativo es que no depende del material.
\[ P = h_{conv} A_s \left(T_s – T_{fluido}\right) \]
Donde \(h_{conv}\) es el coeficiente de confección, \(A_s\) es la superficie en la que se transfiere calor, \(T_s\) es la temperatura de la superficie y \(T_{fluido}\) es la temperatura del fluido. Esta expresión es válida en flujo laminar, lo que en el aire es cierto a temperaturas moderadas (hasta 100 ºC) y cuando las dimensiones de la superficie radiante son pequeñas (hasta 0.5 m).
Refrigeración por convección forzada
Con la convección forzada se puede incrementar hasta un factor 10 la refrigeración por convección. El número de Reynolds (\(R_e\) adimensional) da información sobre qué tipo de fluido tengo.
Dependiendo de la geometría, la región entre flujo laminar y flujo turbulento varía.
Por ejemplo, dentro de un tubo:
- Existirá flujo laminar si \(R_e < 2300 \).
- Existirá flujo turbulento si \(R_e > 10^4 \).
Entre medias de ambos límites existe una frontera poco precisa, por lo que si se trabaja en esta región es recomendable elegir la peor opción para refrigerar. Es decir, flujo laminar. El flujo turbulento es mejor porque el aire va más rápido aunque puede ofrecer más resistencia debido a la fricción.
Para determinar el flujo de calor evacuado, se sigue la expresión:
\[ P = m’ \cdot c_p \cdot \left( T_{out} – T_{in} \right) \]
Con ella se puede determinar m’ (flujo de masa de aire) para saber qué flujo de aire debe mover el ventilador y \(c_p\) es el calor específico del aire.
La convección forzada se rige por la misma expresión que la convección natural. Sin embargo, ahora hay que calcular el coeficiente de convección en función del número de Nussel (Nu, adimensional). El número de Nussel se puede expresar como función del número de Reynolds y el número de Prandtl.
Para determinar la máxima temperatura del aire ambiente a la cual el sistema es posible disipar el calor generado:
- Determinar el flujo de aire a mover para refrigerar una potencia P (m³/s).
- Calcular los CFM del ventilador necesarios utilizando la densidad del aire.
- Calcular el número de Reynolds.
- A partir del número de Reynolds, determinar si el flujo es laminar o turbulento. Laminar: Re < 2300. Turbulento: Re > 10⁴. Entre media, escoger peor caso: laminar.
- En función del tipo de flujo, calcular el número de Nusselt.
- Con el número de Nusselt, calcular el coeficiente de convección \(h_{conv}\).
- Con el \( h_{conv} \), calcular la máxima temperatura del aire del ambiente.
Con la altitud varía la densidad del aire, con lo que el flujo de masa (flujo volumétrico) también.
Si el ventilador se pone a la entrada del sistema, podremos filtrar el aire, aumentará la fiabilidad del ventilador por trabajar con aire fresco pero el calor que genera se añadirá a la carga del sistema.
Si ponemos el ventilador a la salida, el ventilador vivirá menos, no prevendrá que entre aire sucio pero no añadirá calor adicional al sistema.
Los componentes más críticos deben colocarse junto a la entrada de aire y los menos críticos y los que consuman mucha potencia, deben ubicarse a la salida (entendiendo críticos como sensibles a variaciones de temperatura). Hay que buscar la mínima resistencia que los componentes mecánicos y electrónicos oponen al flujo del aire. Buscar que la convección natural ayude y no se oponga a la forzada. Poner en serie dos ventiladores aumenta la presión y hacerlo en paralelo, aumenta el flujo de aire.
Si conocemos la dirección en la que se moverá el aire, disipador de extrusión. Si no, tipo pin-fin.