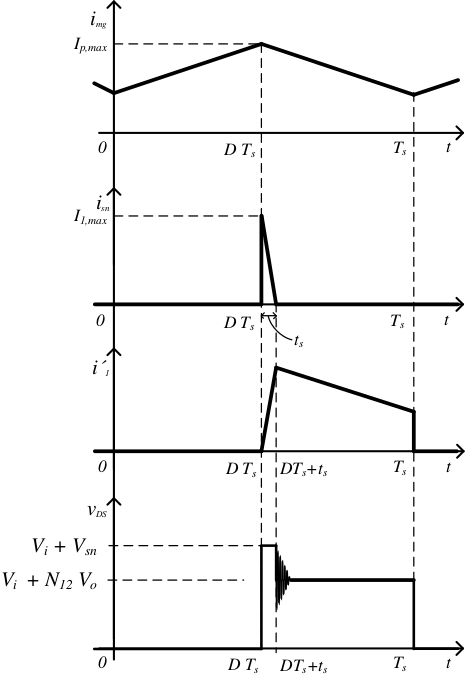
La conmutación de un transistor no es instantánea. Hay momentos en los que la tensión de circuito abierto con la corriente de cortocircuito se solapan dando lugar a picos de potencia. Es lo que se conoce como consumo dinámico del transistor.
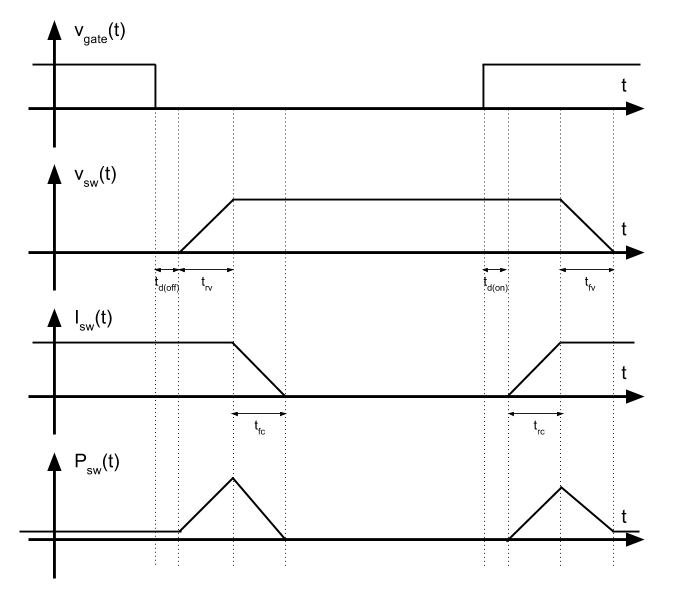
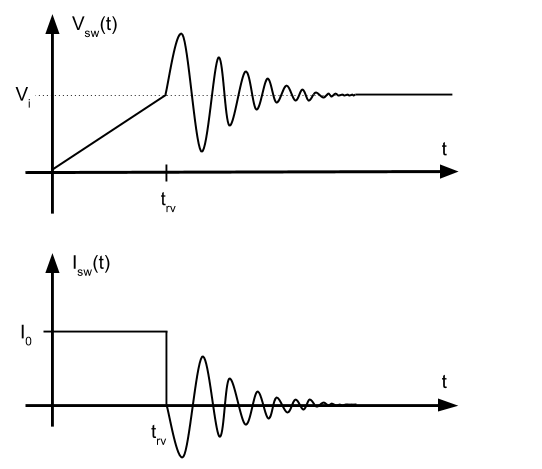
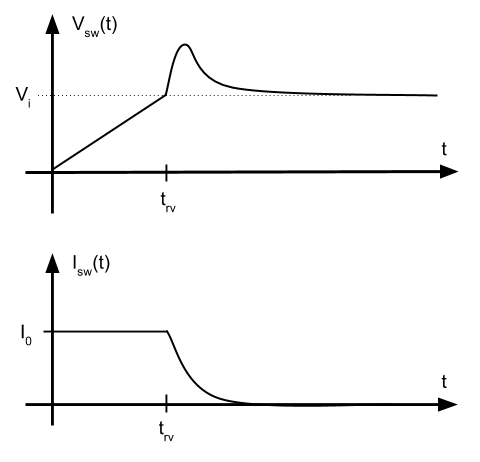
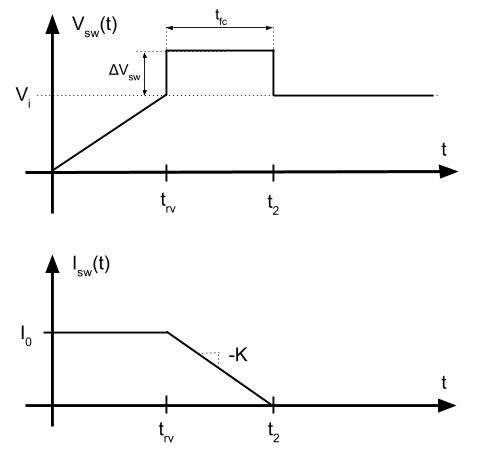
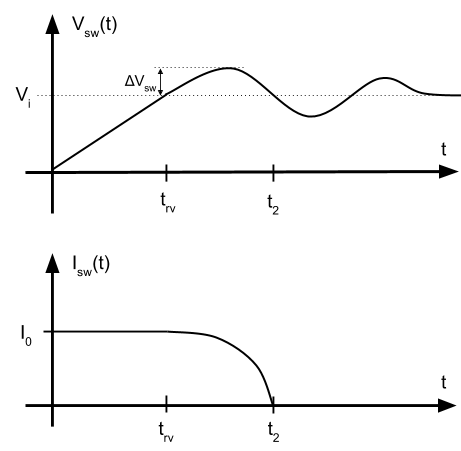
En la imagen vemos como mientras el transistor está en ON, hay un consumo activo debido a la resistencia parásita. Cuando se conmuta a ON o a OFF, aparece un pico de potencia. Una vez puesto a nivel bajo la entrada del transistor, hay un tiempo de retraso (time delay off) y posteriormente la tensión empieza a subir. durante \(t_{rv}\) (time rise voltage) Mientras la tensión sube, la corriente permanece constante. Cuando la tensión termina de subir, entonces la corriente empieza a bajar durante el periodo \(t_{fc}\) (time fall current). Y finalmente vemos que lo mismo ocurre durante la conmutación a ON.
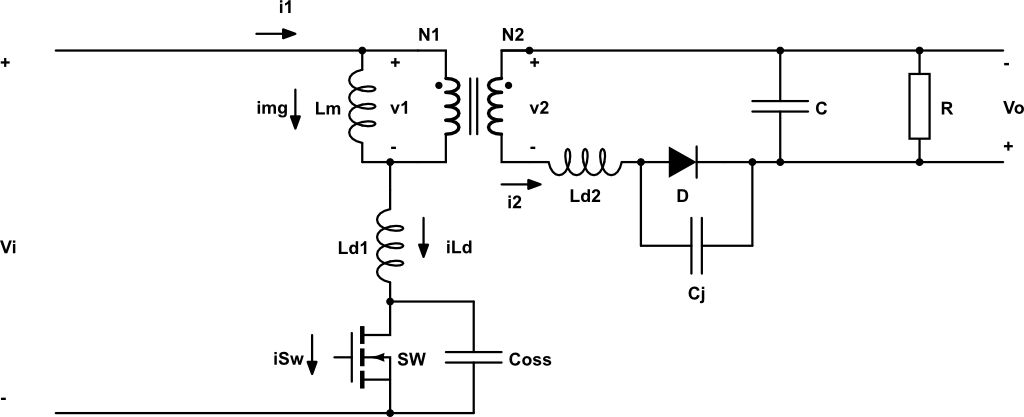
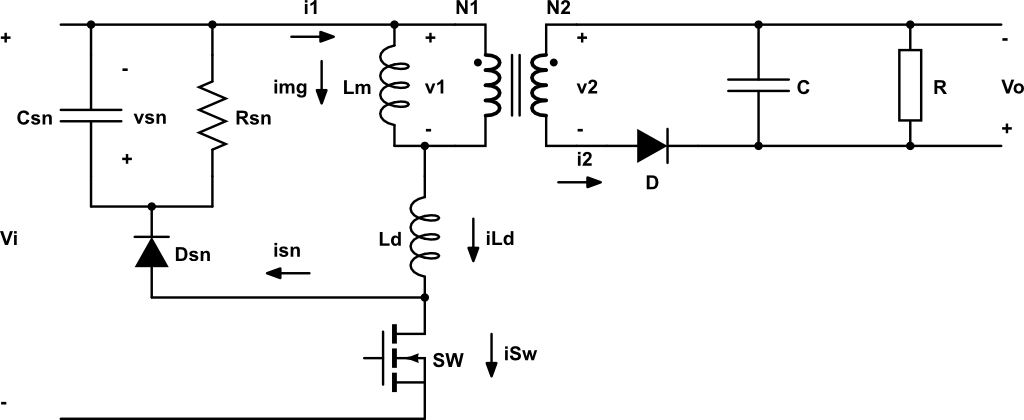
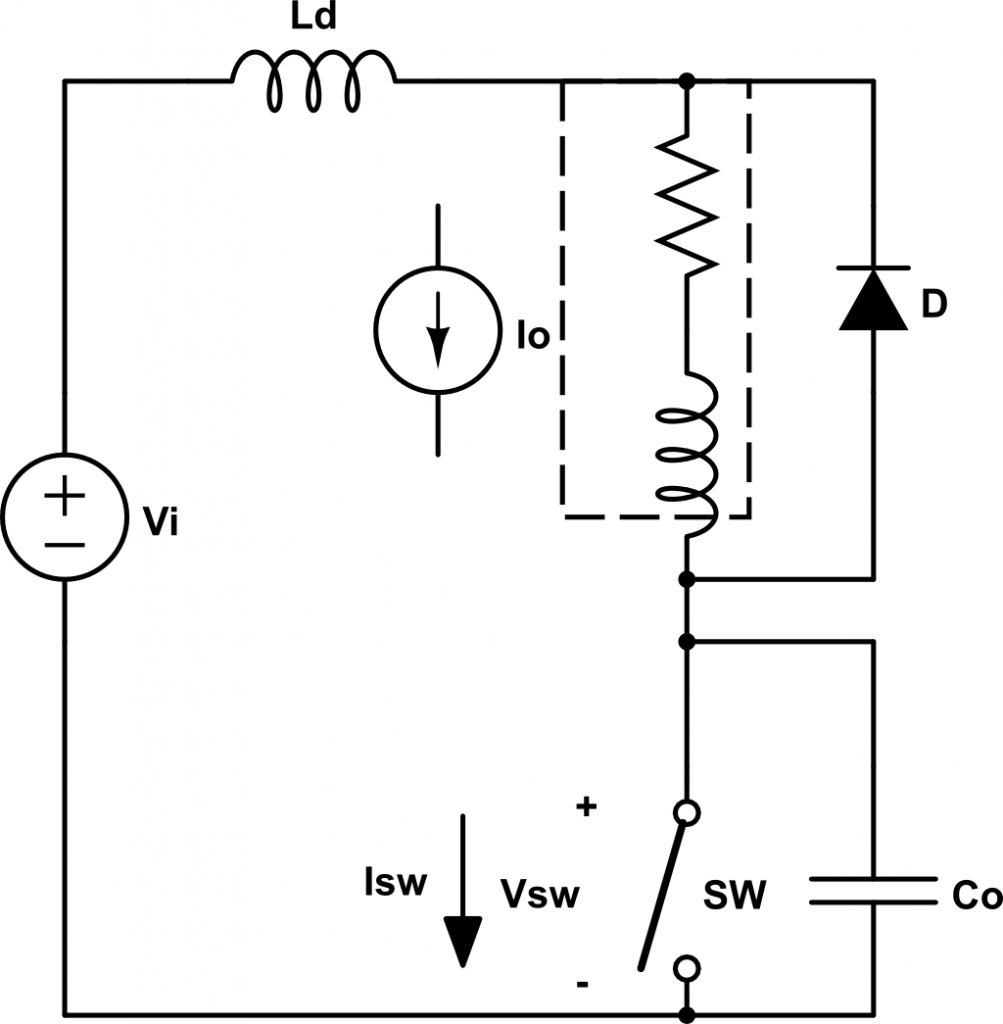
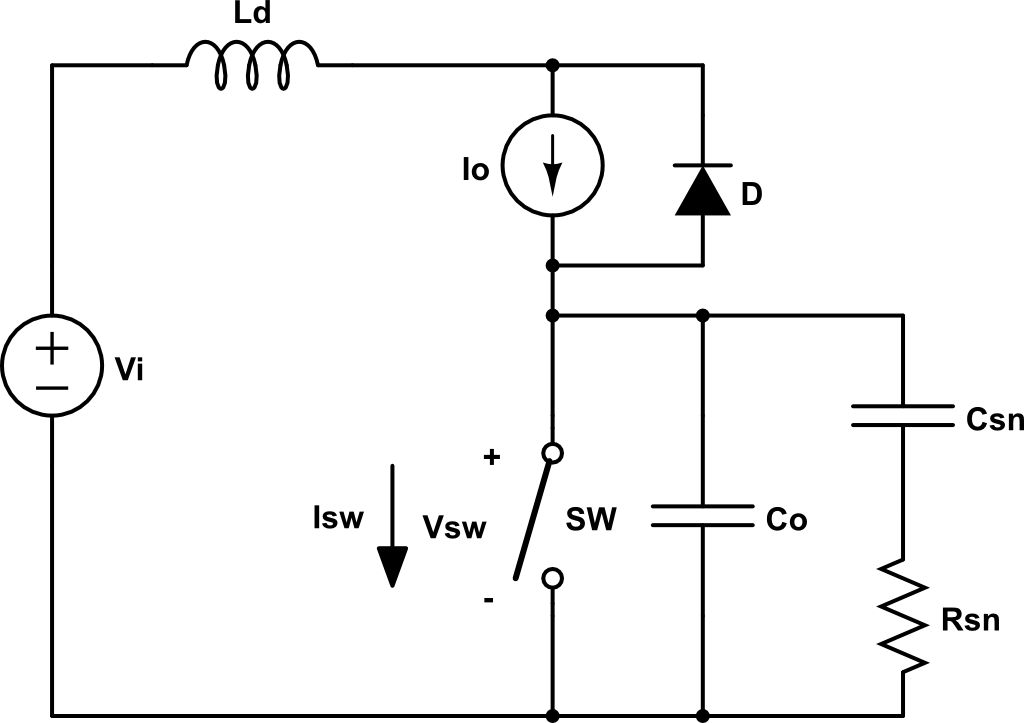
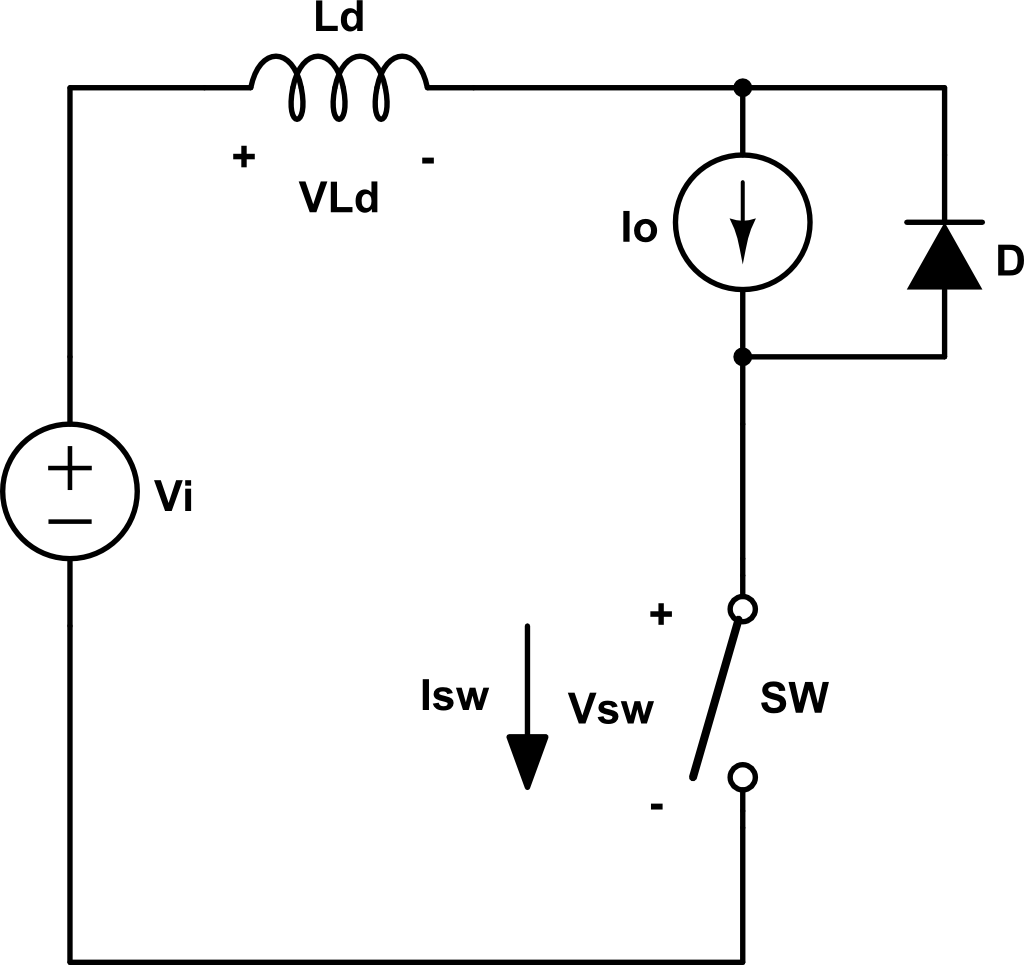
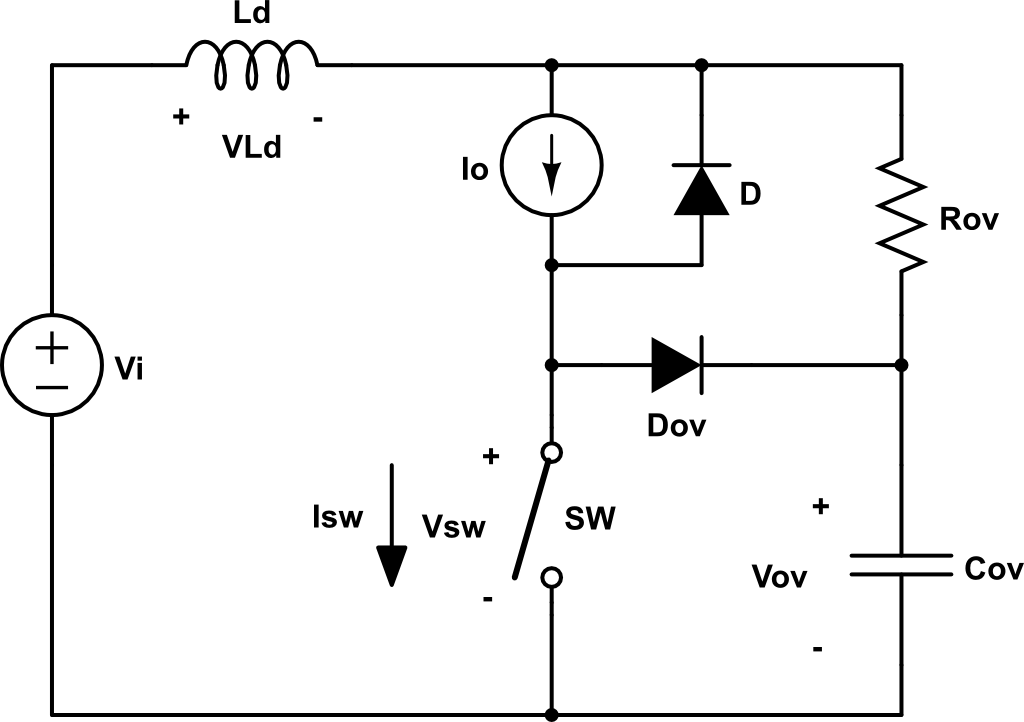
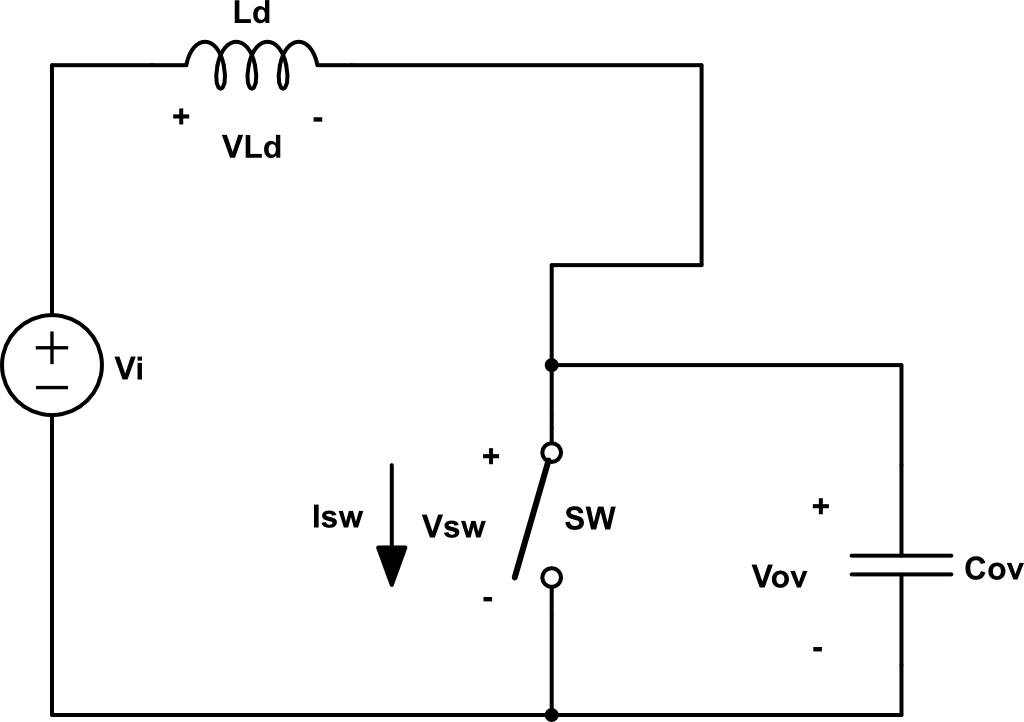
Una red para disminuir la potencia disipada en la conmutación es la siguiente: 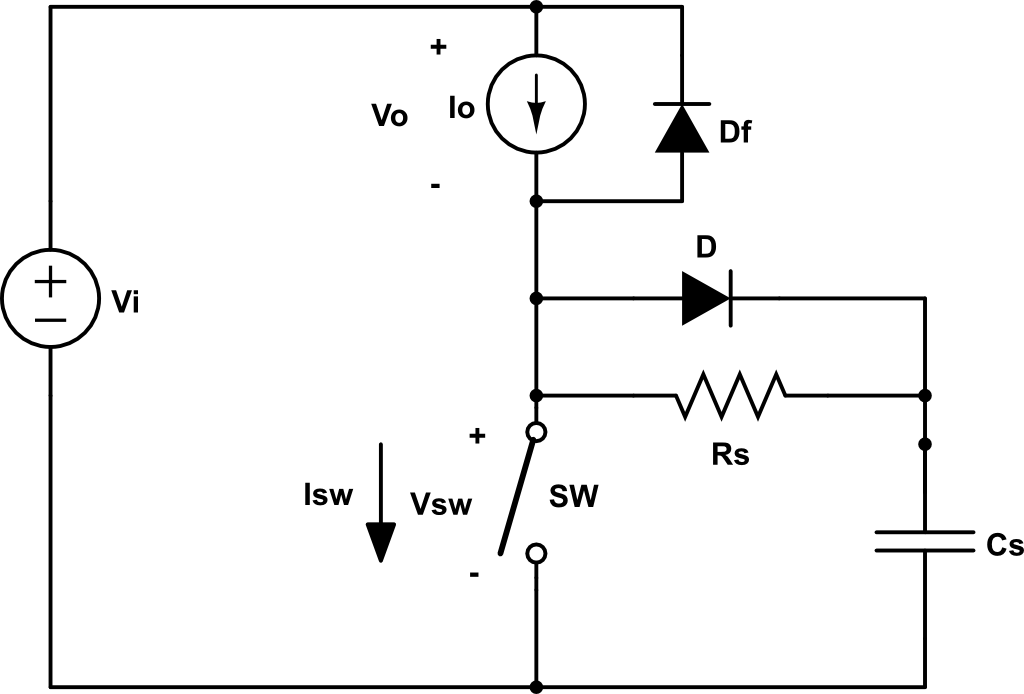
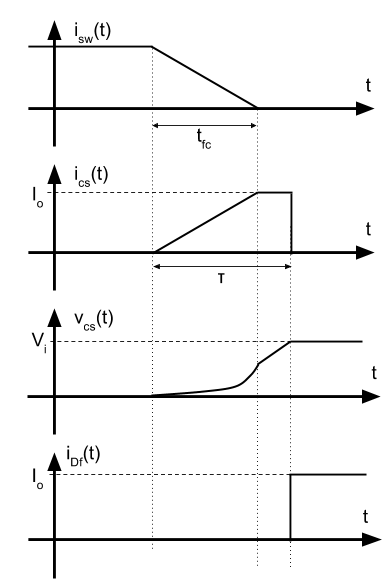
Cuando el SW está ON, \(V_{sw} = 0\), \(V_o = V_i\), \( V_{cs} = 0\), \(i_{sw} = I_o \) y \(i_{Df} = 0 \).
En esta red tenemos dos casos particulares:
- Cuando \(C_s\) es pequeño y \(\tau < t_{fc} \).
- Cuando \(C_s\) es grande y \(\tau > t_{fc} \).
Nota: \(\tau\) no es RC ya que la corriente que carga el condensador no está limitada por la resistencia \(R_s\). Esta resistencia en realidad solo está para descargarlo.
Caso 1)
Intervalo \( 0 < t < \tau \)
\[ i_{sw} = I_o – \frac{I_o}{t_{fi}} t \]
\[ i_{cs} = \frac{I_o}{t_{fi}} \]
\[ V_{cs} = \frac{1}{C_s} \int{i_{C_s} dt} = \frac{1}{C_s} \int_0^\tau{\frac{I_o}{t_{fc}} t dt} = \frac{1}{C_s}\frac{I_o}{t_{fc}}{\frac{\tau^2}{2}} \]
\[V_{cs}(\tau) = V_i = \frac{1}{C_s}\frac{I_o}{t_{fc}}{\frac{\tau^2}{2}} \]
\[ \tau = \sqrt{\frac{2V_i C_s t_{fc}}{I_o}} \] 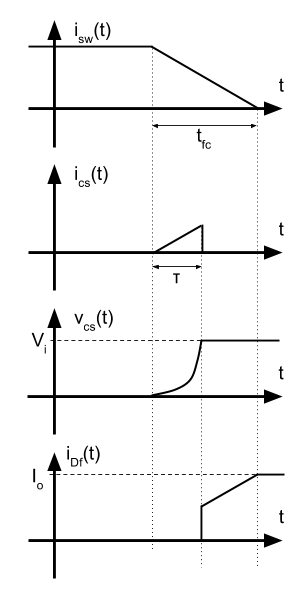
A partir de \(\tau\), el diodo \(D_f\) empieza a conducir:
Intervalo \(\tau\) < t < \(t_{fi}\)
\[ V_{cs} = V_i \]
\[ i_{cs} = 0\]
\[ i_{Df} = I_o – i_{sw} = \frac{I_o}{t_{fc}}t \]
\[i_{Df}(t_1) = \frac{I_o}{t_{fc}}t \]
Caso 2)
Intervalo 0 < t < \(t_{fc}\)
La corriente que pasa por el switch baja:
\[ i_{sw} = I_o – \frac{I_o}{t_{fc}} t \]
La corriente en el condensador sube:
\[ i_{C_s} = \frac{I_o}{t_{fi}} t \]
\[V_{C_s} = \frac{1}{C_s} \int{i_{C_s} dt} = \frac{1}{C_s} \frac{I_o}{t_{fc}} \frac{t^2}{2} \]
\[V_{C_s}(t_{fc}) = \frac{t_{fi}}{2 C_s} \]
Intervalo \(t_{fi} < t < \tau \)
Toda la corriente de la carga circula hacia el condensador, por lo que se carga linealmente.
\[V_{C_s} = \frac{I_o}{C_s} \left( t – t_{fc} \right) + V_{cs}(t_{fc}) \]
\[ V_{C_s} = \frac{1}{C_s} \int{I_o dt}\]
\[V_{C_s} = \frac{I_o}{C_s} \left(\tau-t_{fc}\right) + V_{cs}\left(t_{fc}\right)\]
A la hora de escoger el condensador, se define la constante k, que es la relación entre el tiempo de carga del condensador y el tiempo de bajada de la corriente:
\[ k = \frac{\tau}{t_{fc}}\]
Existe un punto óptimo en el que la potencia que se disipa en la conmutación se minimiza y se da cuando:
\[ k = \frac{2}{3}\]
Hay que tener en cuenta que durante la conmutación a ON la corriente que debe soportar el transistor es la corriente \(I_o\) y la descarga del condensador. Además, es muy importante que durante el tiempo de ON el condensador se descargue totalmente, por lo que esta es la restricción necesario para dimensionar \(R_s\), que sirve para disipar la energía almacenada en el condensador durante el tiempo de ON.
Finalmente, lo que se observa con esta red snubber es que se reduce la tensión que se superpone mientras la corriente todavía está bajando. Por tanto, la potencia disipada en la conmutación se reduce.