The UVM spins around the concept of abstracting the data that is sent and received from the DUT. Data abstraction allows to create and handle complex structures able to describe elaborated scenarios. For instance, we can model a burst I2C writing of 100 bytes without worrying too much about how that is going to be actually implemented. Each byte could be respresented as a transaction and from the TLM perspective we would only need to focus on the meaningful data required for fully describing the operation. Since in UVM each environment component is in charge of different actions (driving, monitoring, arbitring, etc.) a communication mechanism is required for transactions to be sent between the environment components. UVM provides TLM API and classes to do allow such communication.
In this sort of communication there is always a producer and a consumer. However, there are cases where we may want to send the transactions regardless the number of consumers (0, 1 or many). That can be implemented using analysis port and exports and is not the scope of this post.
TLM ports and exports
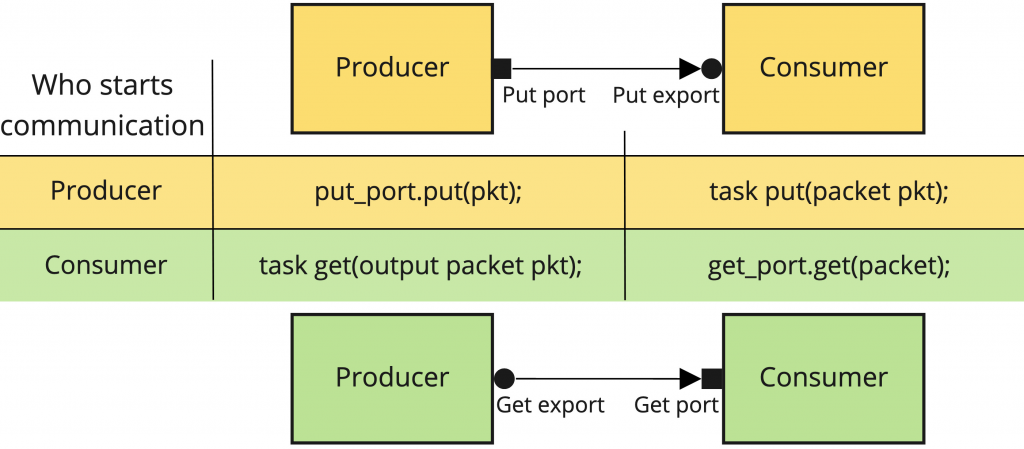
In UVM, a port class provides functions that can be called. Because of this, it will be placed on the component that initiates the communication. As we are going to see soon, the communication can be started by either the consumer or the producer, so the port class has not to be confused with the direction of the transactions.
On the other hand, an export class specifies the implementation of the functions. Therefore, it will be placed on the component that waits for the communication to be started. Again, as in the case of the port, it gives no information per se about the direction of the transactions, only gives information about who asks for them.
The TLM API implements two different ways to control the communication flow. In the case that the communication is started by the producer, then we will need to use a put port. If it is the consumer who controls the communication, then we will use a get port.
Also, an important aspect of the ports and exports is that they require always to be connected. If they remain unconnected then you will have a `uvm_error on simulation time 0 as follows:
UVM_ERROR @ 0: uvm_test_top.env.agent.put_port [Connection Error] connection count of 0 does not meet required minimum of 1Communication started by the producer (put)
In the producer, in order to send a uvm_object, it is necessary to call the put task on the port object.
In the consumer, we need to implement the put task where we can define what we want to do with the incoming transaction. This function will be automatically called when the producer calls the port put task.
Also, there are two different types of put ports: blocking and nonblocking.
UVM TLM blocking put port
The put method implementation is a task and therefore it can consume simulation time. If we call the put method on the producer and want to wait for the consumer to finish processing it before keep executing the producer’s code, then we need a blocking put port. By waiting for the consumer to be done with the transaction sent, we can create synchronization patterns that might be useful for our verification infrastructure.
Producer
The producer calls the put() method over the put_port.
class producer extends uvm_component;
uvm_blocking_put_port #(packet) put_port;
`uvm_component_utils(producer)
function new(string name="producer", uvm_component parent);
super.new(name, parent);
put_port = new("put_port", this);
endfunction
virtual task run_phase(uvm_phase phase);
packet pkt;
pkt = packet::type_id::create("pkt");
if (!pkt.randomize()) `uvm_error("NO_RND", "Couldn't randomize pkt")
put_port.put(pkt);
endtask : run_phase
endclass : producerConsumer
The consumer executes the put() task every time the producer sends a transaction. It is important to know that in the case we need to use the transaction information at a later stage, we need to clone the object so that we hold a copy of it. Otherwise, the transaction data will change as soon as the producer generates a new object since the transaction in the consumer is passed by reference. This can lead to waste an enormous amount of time debugging why the transaction information is not matching the expected values 🙂
class consumer extends uvm_component;
uvm_blocking_put_imp #(packet, consumer) put_export;
`uvm_component_utils(consumer)
function new(string name = "consumer", uvm_component parent);
super.new(name, parent);
put_export = new("put_export", this);
end : new
task put(packet pkt);
// Called everytime the producer sends a transaction
endtask
endclass : consumerFrom the code snippet above, note that the consumer who is finally going to receive the transaction uses a uvm_blocking_put_imp object. Intuitively one can think that a uvm_blocking_put_export should be used, but that’s only used in the case of having multiple layers of communication where we need to connect an export implementation with one or more intermediate layers. Please check out the section «Multiple port/export layers» for more details.
As shown above, the put_port and put_export objects are created inside the class constructor use new and not the UVM factory.
UVM TLM nonblocking put port
If we don’t want to wait for the consumer to have processed and finished the put method before continuing with the program execution in the producer, then we can use a nonblocking put port. To do so, replace in the previous producer and consumer implementation the blocking word with nonblocking when declaring the port and export.
Communication started by the consumer (get)
In the case of being the consumer who will ask for transactions, then we will need to create an export in the producer and a port in the consumer.
UVM TLM blocking get port
class producer extends uvm_component;
uvm_blocking_get_imp #(packet, producer) get_export;
`uvm_component_utils(producer)
function new(string name="producer", uvm_component parent);
super.new(name, parent);
get_export = new("get_export", this);
endfunction
task get(output packet pkt);
pkt = packet::type_id::create("pkt");
if (!pkt.randomize()) `uvm_error("NO_RND", "Couldn't randomize pkt")
endtask : get
endclass : producerclass consumer extends uvm_component;
uvm_blocking_get_port #(packet) get_port;
`uvm_component_utils(consumer)
function new(string name = "consumer", uvm_component parent);
super.new(name, parent);
get_port = new("get_port", this);
end : new
virtual task run_phase(uvm_phase phase);
Packet pkt;
[...]
get_port.get(pkt);
endtask : run_phase
endclass : consumerUVM TLM nonblocking get port
If we don’t want to wait for the producer to send the packet before continuing with the program execution in the consumer, then we can use a nonblocking get port. To do so, again, replace in previous producer and consumer implementation the blocking word with nonblocking when declaring the port and export.
| Method | Blocking | Nonblocking | |
|
Put
|
Port | uvm_blocking_put_port#(tr) |
uvm_nonblocking_put_port#(tr)
|
| Export | uvm_blocking_put_export#(tr) |
uvm_nonblocking_put_export#(tr)
|
|
| Imp | uvm_blocking_put_imp#(tr, parent) |
uvm_nonblocking_put_imp#(tr, parent)
|
|
|
Get
|
Port | uvm_blocking_get_port#(tr) |
uvm_nonblocking_get_port#(tr)
|
| Export | uvm_blocking_get_export#(tr) |
uvm_nonblocking_get_export#(tr)
|
|
| Imp | uvm_blocking_get_imp#(tr, parent) |
uvm_nonblocking_get_imp#(tr, parent)
|
The rest of the component implementation remains the same.
Connecting ports and exports
Both port and export have to be connected together using the connect() method. This is usually done at a higher hierarchy level, i.e., the producer and/or consumer parent. For instance, in order to connect an agent’s driver with the sequencer, the connection will be done on the agent’s class on the connect_phase().
The connect() method is implemented on the port object. Therefore, the depending on the put or get method used we will need to call the connect() over the producer or the consumer. In the example below, both cases are shown. However, bear in mind that only one actually applies for connect a TLM port and export.
class pkt_agent extends uvm_agent;
producer prod;
consumer cons;
`uvm_component_utils(pkt_agent)
[...]
virtual function void build_phase(uvm_phase phase);
[...]
prod = producer::type_id::create("prod", this);
cons = consumer::type_id::create("cons", this);
endfunction : build_phase
virtual function void connect_phase(uvm_phase phase);
super.connect_phase(phase);
// Put port/export. It does not apply on get method
prod.put_port.connect(cons.put_export);
// Get port/export. It does not apply on put method
cons.get_port.connect(prod.get_export);
endfunction : connect_phase
endclassMultiple port/export layers
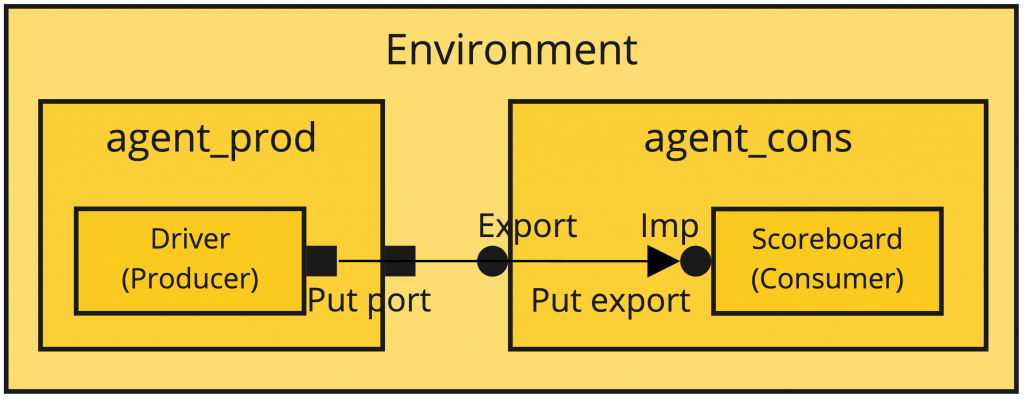
In case of having multple port/export layers, such as the case depicted below, we need to connect ports with ports and exports with exports in the highest levels of hierarchy.
When driving the transaction outwards, we will use a port. When driving the transaction inwards AND it is not the last component, we will use an export. And finally, when driving the transaction into the last component (the destination), we will use an imp (since it is the place where we will implement the put or get method).
In this case, the connections will be done as follows:
- Port to port: child_comp.child_port.connect(parent_port)
- Port to export: put_port_comp.put_port.connect(export_port_comp.export_port)
- Export to export: parent_comp.parent_port.connect(child_port.export)
An example implementating the diagram above can be:
class agent_prod extends uvm_agent;
driver drv; // Let's assume the driver has a uvm_blocking_put_port#(packet) object
uvm_blocking_put_port put_port;
`uvm_component_utils(agent_prod)
function new(string name="agent_prod", uvm_component parent);
super.new(name, parent);
put_port = new("put_port", this);
endfunction
virtual function void connect_phase(uvm_phase phase);
super.connect_phase(phase);
drv.put_port.connect(put_port);
endfunction : connect_phase
endclass : agent_prod
class agent_cons extends uvm_agent;
scoreboard scb; // Let's assume the scoreboard has a uvm_blocking_put_imp#(packet, scoreboard) object
uvm_blocking_put_export#(packet) put_export;
`uvm_component_utils(agent_cons)
function new(string name="agent_cons", uvm_component parent);
super.new(name, parent);
put_export = new("put_export", this);
endfunction
virtual function void connect_phase(uvm_phase phase);
super.connect_phase(phase);
put_export.connect(scb.put_export);
endfunction : connect_phase
endclass : agent_cons
class env extends uvm_env;
agent_prod agent_port;
agent_cons agent_exp;
`uvm_component_utils(env)
function new(string name, uvm_component parent);
super.new(name, parent);
endfunction
function void build_phase(uvm_phase phase);
agent_port = agent_prod::type_id::create("agent_port", this);
agent_exp = agent_cons::type_id::create("agent_exp", this);
endfunction
function void connect_phase(uvm_phase phase);
super.connect_phase(phase);
agent_port.put_port.connect(agent_exp.put_export);
endfunction
endclass