Mes: abril 2022

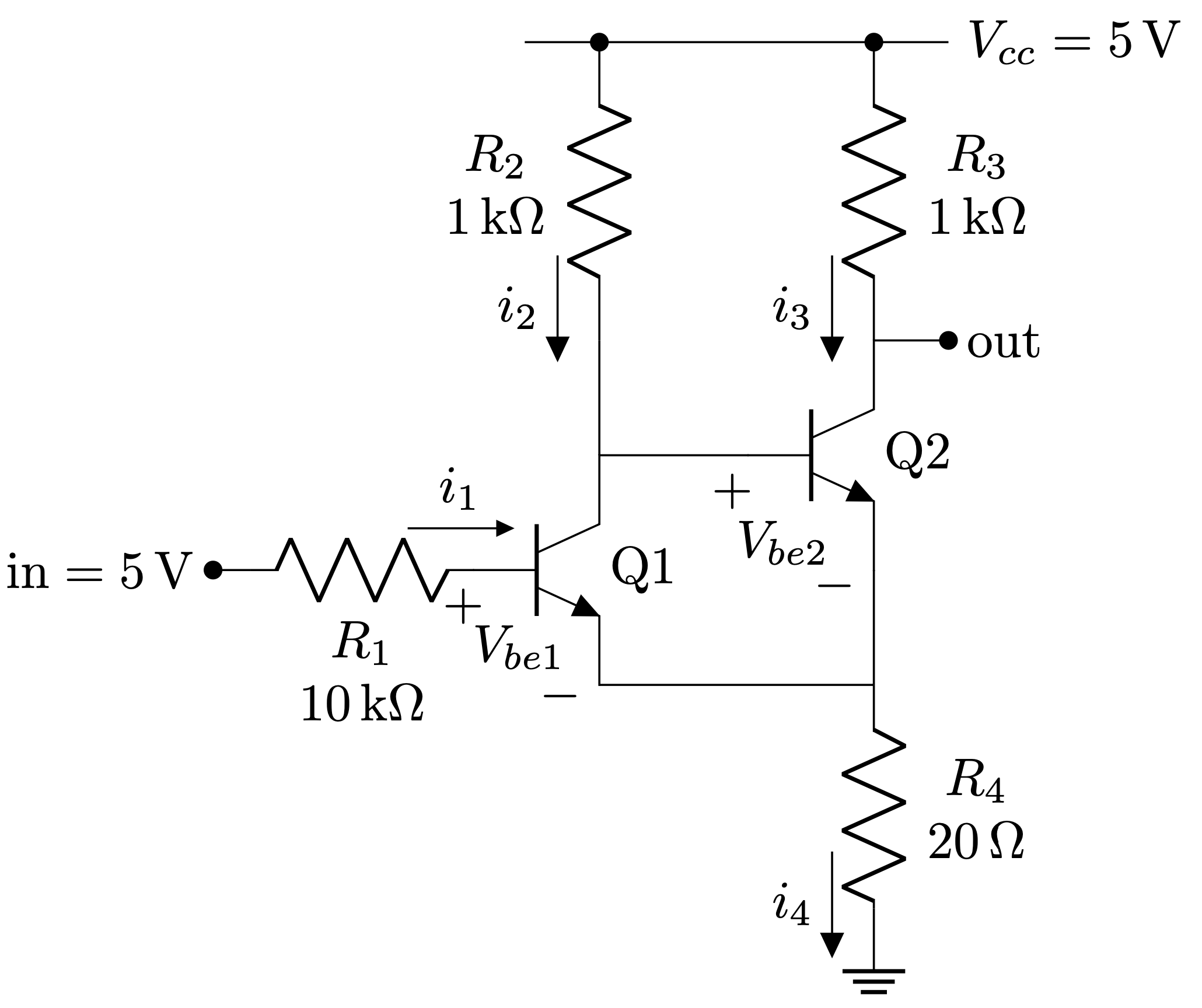
The following circuit is known as a Schmitt trigger, implemented with BJT transistors. The main purpose of a Schmitt trigger is to generate a digital signal, which stated in other words is a signal whose only possible values are \(V_{cc}\) (logic 1) or ground (logic 0). The original analog signal can vary slowly in time so that the transition periods from high/low to low/high might not be fast enough. This circuit will act as a comparator with hysteresis whose thresholds for setting the output high or low will be defined by the design parameters.

Throughout the analysis we are going to consider for simplicity a voltage \(V_{be} = 0.6~V\) for the NPN to leave cut off and \(V_{ce} = 0.0~V\) when in saturation.

Since \(v_{in} = 5V\), \(Q_1\) is in saturation and in turn \(Q_2\) is cut off, then: \[i_2 = \frac{5~V}{1~k\Omega + 20~\Omega} = 4.9~mA\] \[i_3 = 0~mA\]\[v_{out} = 5~V\]\[v_{e} = i_2 \cdot R_4 = 4.9~mA · 20~\Omega = 98~mV\] \[v_{b1} = v_e + v_{be1} = 98~mV + 0.6~V \approx 0.7~V\]

A couple of details that can be extracted from here:

  • By having a voltage able to take \(Q_1\) into saturation, the output goes to \(V_{cc}\).
  • In order to get \(Q_1\) cut off, we need to drop \(in\) approximately \(100~mV\) higher than the \(v_{be}\) voltage, i.e., \(Q_1\) would cut off around \(in \approx 0.7~V\).

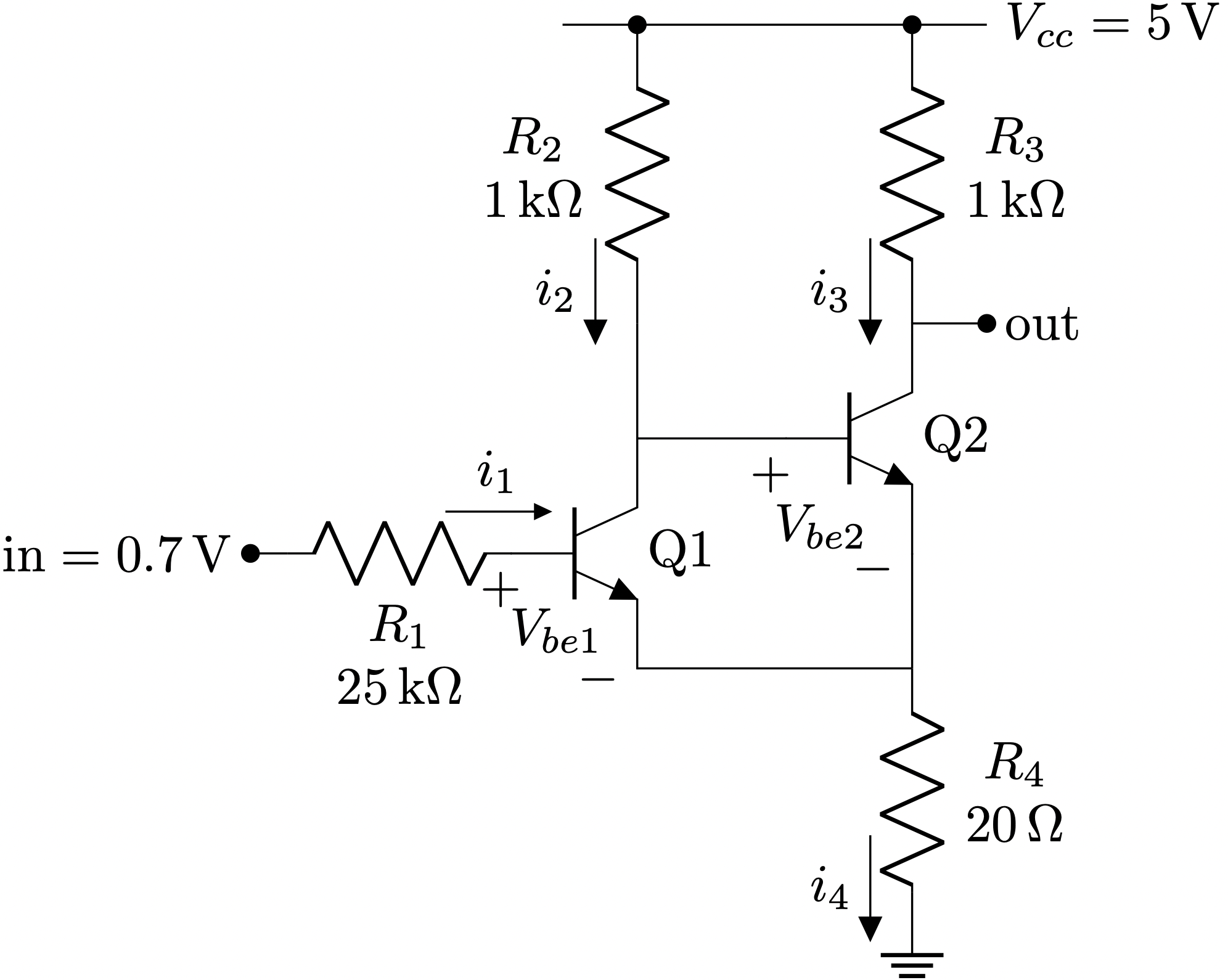
Therefore, let’s see what happens when from \(in = 5~V\) we drop \(in\) to \(0.7~V\).

\(Q_1\) and \(Q_2\) were in saturation and cut off respectively.
However, now that \(in = 0.7~V\), \(Q_1\) starts to stop driving current.
This makes the voltage at \(V_{b2}\) to rise due to a lower voltage drop across \(R_2\) and \(Q_2\) enters in saturation.
Since \(Q_2\) is in saturation, \(v_{be} = 0.6~V\)

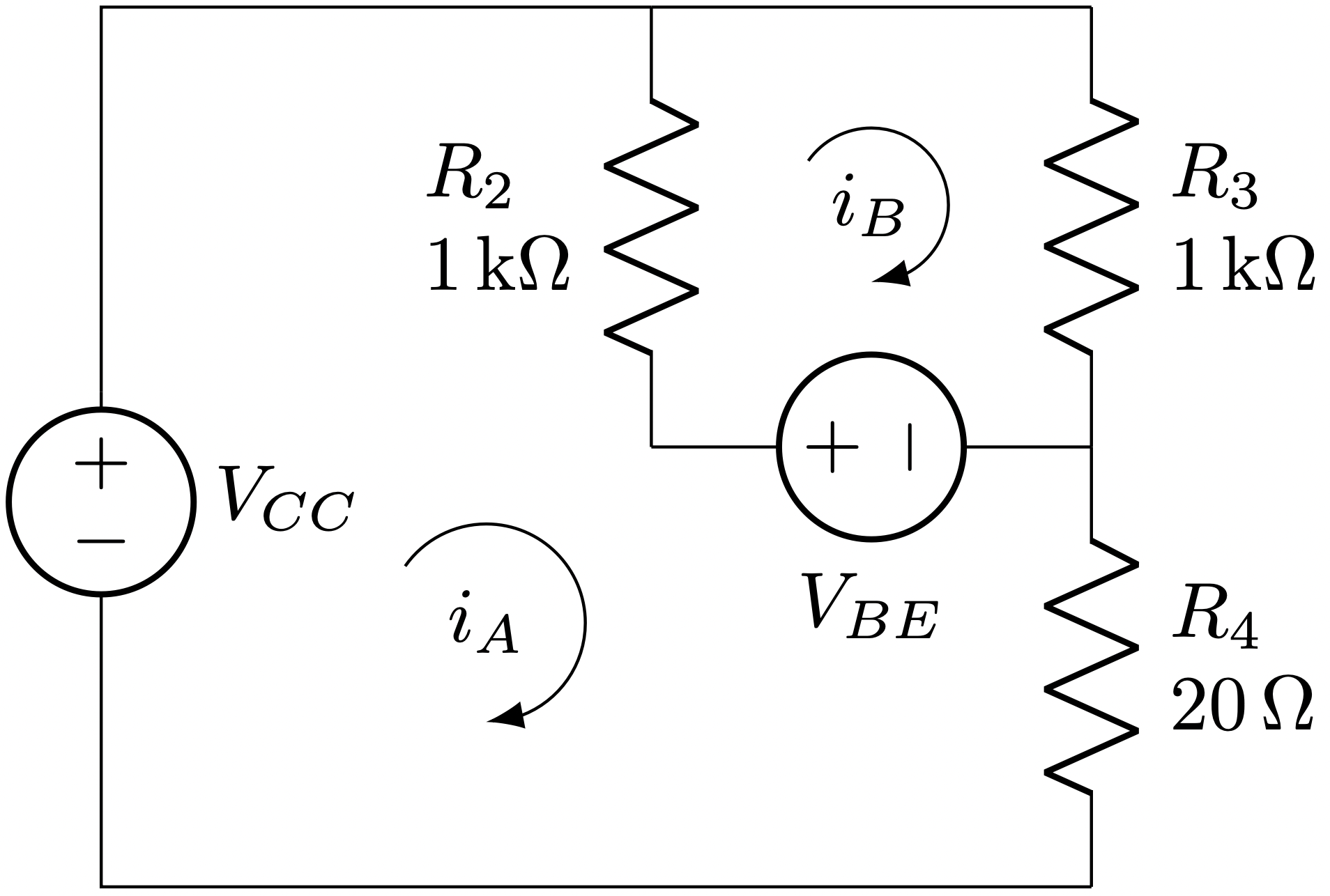
In order to compute the currents going through the circuit in this state we can perform a mesh analysis taking into account the \(V_{BE}\) voltage between the base and the emitter and considering \(V_{CE} = 0\).

The two equations from meshes A and B are:
\[-V_{cc} + \left(R_2 + R_4\right)\cdot i_A + V_{be} – R_2\cdot i_B = 0\] \[-V_{be} – R_2\cdot i_A + \left(R_2 + R_3\right)\cdot i_B = 0\] Which can be written in matrix form as:\[\begin{pmatrix}
R_2 + R_4 & -R_2 \\
-R_2 & R_2 + R_3 \\
\end{pmatrix}
\begin{pmatrix}
i_A\\
i_B\\
\end{pmatrix} =
\begin{pmatrix}
V_{cc} – V_{be} \\
V_{be}
\end{pmatrix}\] Solving this equation as \(X = A^{-1} B\) we get that:\[i_A = 9.03~mA,~~ i_B = 4.81~mA\]With these current values, the voltage at the Q2 emitter is: \[V_{e} = i_A \cdot R_4 = 9.03~mA \cdot 20~\Omega = 180.6~mV\]

Again, what we can extract from these results is:

  • By having a voltage able to set \(Q_1\) cut off, the output goes to \(180~mV\), which in most of the digital families such as TTL or CMOS can be safely considered as a logic 0.
  • In order to get \(Q_1\) in saturation again, we need to increase \(in\) approximately \(180~mV\) above the \(v_{be} = 0.6\) voltage, i.e., \(Q_1\) would saturate around \(in \approx 0.78~V\).

So as we can see the circuit has hysteresis since thresholds for low to high and high to low are placed at different input voltages. This effect avoids having potentially multiple toggles at the output when the input voltage is near the threshold if the threshold would have been the same in both cases (low to high and high to low). Finally, the hysteresis voltage \(\Delta V\) can be approximated as \(\Delta V = \frac{R4}{R3} \cdot V_{cc}\).

LaTeX used to generate this article’s images:

\begin{circuitikz}
	\ctikzset{transistors/arrow pos=end}
	\draw (0,0) node[npn] (Q1){Q1};
	\draw (Q1.B) to[R, l2=$R_1$ and \SI{25}{\kilo\ohm}, l2 halign=c] ++(-1.5, 0) coordinate(in);
	\draw (in) to[short, -*] ++(-0.25,0) node[left]{in};
	\draw (Q1.C) -- +(1,0) node[npn, anchor=B](Q2){Q2} ;
	\draw (Q2.E) -- (Q2.E |- Q1.E);
	\draw (Q1.E) -- (Q1.E -| Q2.E);
	\draw (Q2.C) to[short, -*] +(0.5, 0) node[right]{out};
	\draw (Q1.E -| Q2.E) -- +(0, -0.25) to[R, l2=$R_4$ and \SI{20}{\ohm}] ++(0, -1.5) node[ground]{};
	\draw (Q1.C) -- (Q1.C |- Q2.C);
	\draw (Q1.C |- Q2.C)  to[R, l2=$R_2$ and \SI{1}{\kilo\ohm}, -*] ++(0, 2) coordinate(R2_top);
	\draw (Q2.C) to[R, l2_=$R_3$ and \SI{1}{\kilo\ohm}, -*] ++(0, 2) coordinate (R3_top);
	\draw (R3_top) -- (R2_top) -- +(-0.5, 0);
	\draw (R3_top) -- +(0.5, 0)  node[right]{$V_{cc}$};
\end{circuitikz}
\begin{circuitikz}
        \ctikzset{transistors/arrow pos=end}
	\draw (0,0) node[npn] (Q1){Q1};
	\draw (Q1.B) to[R, l2=$R_1$ and \SI{10}{\kilo\ohm}, l2 halign=c, f<_=\SI{430}{\micro\ampere}, current arrow scale=24] ++(-1.5, 0) coordinate(in);
	\draw (Q1.B) node[below, xshift=-2]{$+$};
    \draw (Q1.E) node[anchor=south east, yshift=-9]{$-$};
    %\draw ($(Q1.B)!0.5!(Q1.E)$) coordinate(vbe_label);
    %\draw (vbe_label) node[yshift=-3, xshift=-2]{$V_{be1}$};
    \draw (Q1) node[anchor=north east, yshift=-7, xshift=-3]{$V_{be1}$};
	\draw (in) to[short, -*] ++(-0.25,0) node[left]{$\text{in} = \SI{5}{\volt}$};
	\draw (Q1.C) -- +(1,0) node[npn, anchor=B](Q2){Q2} ;
	\draw (Q2.E) -- (Q2.E |- Q1.E);
	\draw (Q1.E) -- (Q1.E -| Q2.E);
	\draw (Q2.C) to[short, -*] +(0.5, 0) node[right]{out};
	\draw (Q2.B) node[below, xshift=-3]{$+$};
    \draw (Q2.E) node[left, yshift=-3]{$-$};
	\draw (Q2) node[anchor=north east, yshift=-9, xshift=-5]{$V_{be2}$};
	\draw (Q1.E -| Q2.E) -- +(0, -0.25) coordinate(R4_top) to[R, l2=$R_4$ and \SI{20}{\ohm}, f_=\SI{5.43}{\milli\ampere}, l2 halign=c] ++(0, -1.5) node[ground]{};
	\draw (Q1.C) -- (Q1.C |- Q2.C);
	\draw (Q1.C |- Q2.C)  to[R, l2=$R_2$ and \SI{1}{\kilo\ohm}, -*, f<^=\SI{4.9}{\milli\ampere}, l2 halign=c] ++(0, 2) coordinate(R2_top);
	\draw (Q2.C) to[R, l2_=$R_3$ and \SI{1}{\kilo\ohm}, -*, f<^=\SI{0}{\milli\ampere}, l2 halign=c] ++(0, 2) coordinate (R3_top);
	\draw (R3_top) -- (R2_top) -- +(-0.5, 0);
	\draw (R3_top) -- +(0.5, 0)  node[right]{$V_{cc}=\SI{5}{\volt}$};
\end{circuitikz}
\begin{circuitikz}
	\draw (0, 0) to[R, l2_=$R_2$ and \SI{1}{\kilo\ohm}] +(0, -2) coordinate(R2_bottom);
	\draw (R2_bottom) to[vsource, l_=$V_{BE}$]  +(2, 0) coordinate(QB);
	\draw (R2_bottom -| QB) to[R, l2_=$R_3$ and \SI{1}{\kilo\ohm}] +(0, 2) coordinate(R3_top);
	\draw (QB) to [R, l=$R_4$, l2=$R_4$ and \SI{20}{\ohm}] +(0, -2) coordinate (R4_bottom);
	\draw (0,0) -- (R3_top);
	\draw (0,0) -- (-2.5, 0) -- (-2.5, -1.75);
	\draw (-2.5, -1.75) to[vsource, l=$V_{CC}$] +(0, -1.0) coordinate(Vcc_bottom) -- (R4_bottom -| Vcc_bottom) -- (R4_bottom);
	 \draw [Latex-]  (1.0,-1.25) coordinate(loop) node [anchor=center, yshift=10] {$i_B$} arc (-90:145:3.5mm);
	 \draw [Latex-]  (-0.75,-3.25) coordinate(loop) node [anchor=center, yshift=13] {$i_A$} arc (-90:145:4.5mm);
\end{circuitikz}

The LaTeX package CircuiTikZ is an excelent way to draw circuits in a standard and elegant manner. However, it can get quite tricky when you need to specify the absolute coordinates of all the nodes of your schematic.

In order to facilitate this process coordinates and orthogonal coordinates come to the rescue.

Coordinates

You can provide a name for every node in your circuit. For instance, in the following line:

\draw (0,0) -- (2,0) coordinate(pointA);

point (2,0) can be accessed from now on using (pointA):

\draw (0,0) -- (2,0) coordinate(pointA);
\draw (pointA) to[R] ++(2,0);

The resistor will be placed from pointA, i.e., (2,0), to (4,0). Remember that the operator ++() makes a relative movement with respect the previous point (in this case (2,0)) and «stores» the position so that any new component in the same \draw statement will start from that point, i.e., (4,0). Also, +() makes the relative movement with respect the original point without storing the new position and not affecting any subsequent element in the \draw statement.

When using hardcoded coordinates like in previous example it might not be very powerful per se, but at least it may help to understand the way the diagram is written.

However, they can solve a lot of headaches when you need to draw two or more components in parallel.

Orthogonal coordinates

In case you want to align to different nodes, orthogonal coordinates computes automatically the X and Y of the new node.

From CircuiTikZ manual, section 2.2, where a classic non-inverting amplifier using an op amp is being drawn:

\draw (FB) to[R=$R_2$] (FB -| OA.out) -- (OA.out)

The way the previous line can be read is:

  1. From the coordinate FB, add a resistor to
  2. The horizontal value of FB (that’s why - is next to FB) and the veritical of OA.out (that’s why | is before OA.out)
  3. Then draw a line from this previous point to the op amp output OA.out

Example

Below you will find an example where all previous concepts are applied in order to draw the schematic of a basic pulse generator with BJT’s.

\usepackage[american]{circuitikz}
\usepackage{siunitx}

\begin{circuitikz} []
   \draw (0,0) node[bjtnpn] (Q1){Q1};
   \draw (Q1.B) to[R, l2={$R_1$ and \SI{10}{\kilo\ohm}}, l2 halign =c] ++(-2,0) to[short,-o] ++(-0.1, 0) node[above]{in};
   \draw (Q1.C) to[R, l2={$R_2$ and \SI{1}{\kilo\ohm}}] ++(0, 2) coordinate(R2t);
   \draw (Q1.E) to[short] ++(0, -0.1) coordinate(Q1gnd) node[ground] (GND){} ;
   \draw (Q1.C) to[C, l2_=$C_1$ and \SI{10}{\nano\farad}, l2 halign =c] ++(2.5,0) coordinate(c1n) to[short] +(0,-1) node[bjtnpn, anchor=B](Q2){Q2};
   \draw (c1n) to[R,l2=$R_3$ and \SI{10}{\kilo\ohm}] ++(0,2) coordinate (R3t);
   \draw (R2t) -- (R3t);
   \draw (R2t) -- +(-0.5,0);
   \draw (R3t) -- +(0.5, 0);
   \draw (Q2.E) -- (Q2.E |- Q1gnd) node[ground]{};
   \draw (Q2.C) -- (Q2.C |- c1n) coordinate(R4b) to[R,l2_=$R_4$ and \SI{1}{\kilo\ohm}] (Q2.C |- R2t) coordinate(R4t) -- (R3t);
   \draw (R4t) -- ++(0.5,0);
   \draw (Q2.C) to[short, -o] ++(1,0) node[above]{out};
\end{circuitikz}