Introducción
Los convertidores conmutados consumen corrientes armónicas. Esto causa que la corriente que la red entrega a la carga no tenga la misma forma que la tensión, o dicho de otro modo, que la frecuencia de la corriente sea diferente de la fundamental. Esto produce tanto distorsión armónica en la corriente suministrada por la red como distorsión de la tensión en el punto de conexión. Este último efecto es debido a que la línea tiene una impedancia distinta de 0 a la frecuencia de los armónicos y se produce una caída de tensión.
Para corregir esta situación, se pueden filtrar los armónicos de la corriente mediante redes pasivas resonantes o también se pueden emplear filtros activos en serie o en paralelo mediante inversores. Sin embargo, estas medidas son complicadas o no resuelven el problema de fondo que es que el convertidor está consumiendo corriente de manera poco eficiente.
Por ello, la mejor estrategia para solucionar este problema es utilizar rectificador de alto factor de potencia (HPF), los cuales reducen el consumo de armónicos de baja frecuencia en lugar de intentar atenuar los existentes. Este tipo de rectificadores modifican la forma de onda de la corriente de entrada para mejorar el espectro armónico y el factor de potencia. Existen varias maneras de clasificar un rectificador HPF: según la forma de la corriente absorbida (totalmente sinusoidal o simplemente se ajusta al máximo establecido por la normativa), según el número de semiconductores o según el estrés que sufren los semiconductores. (control en conducción continua, control en conducción discontinua o en el límite entre c.c. y c.d. o convertidores con redes resonantes para ZVS y ZCS).
Los rectificador HPF cuentan en esencia de dos etapas: la pre-regulación y la post-regulación.
Pre-regulador monofásico HPF. Rectificador + Convertidor DC/DC
El funcionamiento ideal del rectificador sería aquel en que la corriente que obtiene de la red debe ser sinusoidal y debe estar en fase con la tensión. Esto solo ocurre si la carga conectada a la salida del rectificador tiene un comportamiento idealmente resistivo.
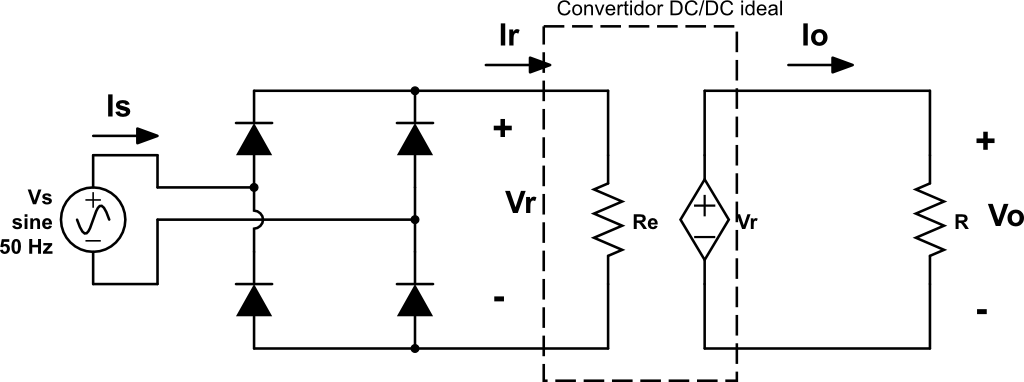 Como vemos en la figura de arriba, si el rectificador ve conectado a su salida una resistencia, en este caso \(R_e\), la corriente será sinusoidal y estará en fase con la tensión.
Como vemos en la figura de arriba, si el rectificador ve conectado a su salida una resistencia, en este caso \(R_e\), la corriente será sinusoidal y estará en fase con la tensión.
\[ i_r(t) = \frac{v_r(t)}{R_e}\]
En este caso, de manera ideal, la potencia que llega a la resistencia emulada (\(R_e\)) es transferida sin pérdidas a la carga \(R\). De manera que se cumple que:
\[ p(t) = \frac{v^2_r}{R_e} = \frac{V^2_o}{R} \]
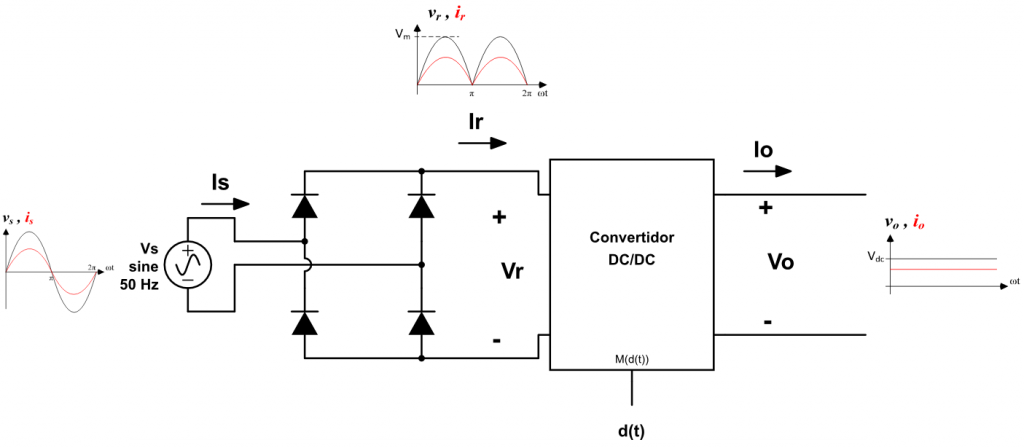 El convertidor DC/DC deberá actuar de forma dinámica variando el ciclo de trabajo para obtener una tensión de salida constante a partir de la tensión de entrada variable. Por tanto, la relación de transformación \(M(d(t))\) será:
El convertidor DC/DC deberá actuar de forma dinámica variando el ciclo de trabajo para obtener una tensión de salida constante a partir de la tensión de entrada variable. Por tanto, la relación de transformación \(M(d(t))\) será:
\[ M\left( d(t) \right) = \frac{v_o(t)}{v_r(t)} = \frac{V_{DC}}{V_m\left|\sin(\omega t)\right|} \]
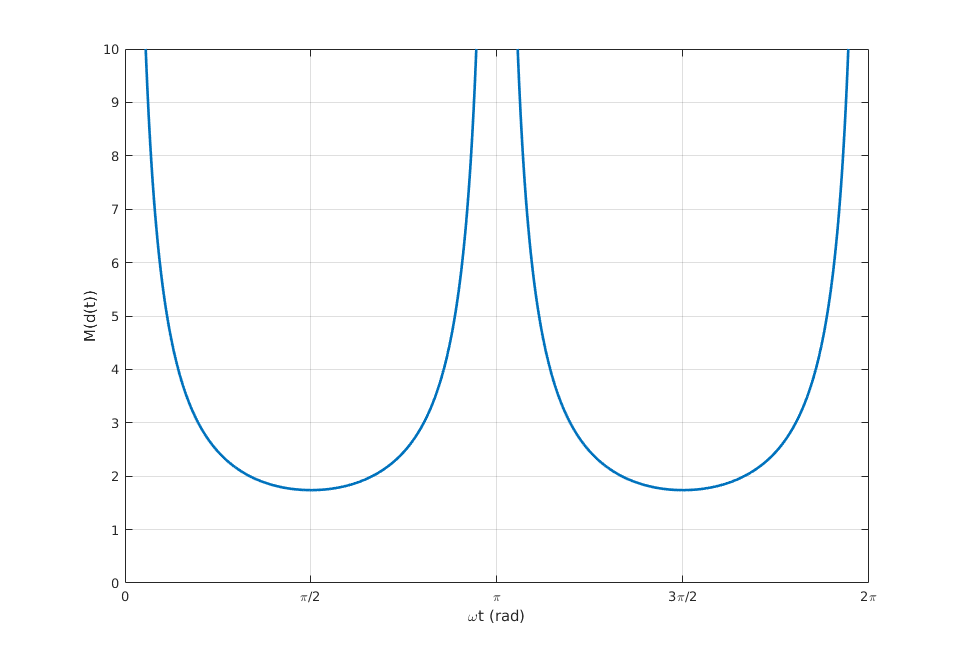 Por tanto, cualquier convertidor que sea capaz de tener esta función de transferencia, podrá generar una tensión continua a la salida obteniendo de la red una corriente con forma sinusoidal y en fase con la tensión.
Por tanto, cualquier convertidor que sea capaz de tener esta función de transferencia, podrá generar una tensión continua a la salida obteniendo de la red una corriente con forma sinusoidal y en fase con la tensión.
Las formas de onda de la tensiones y las corrientes en el convertidor son:
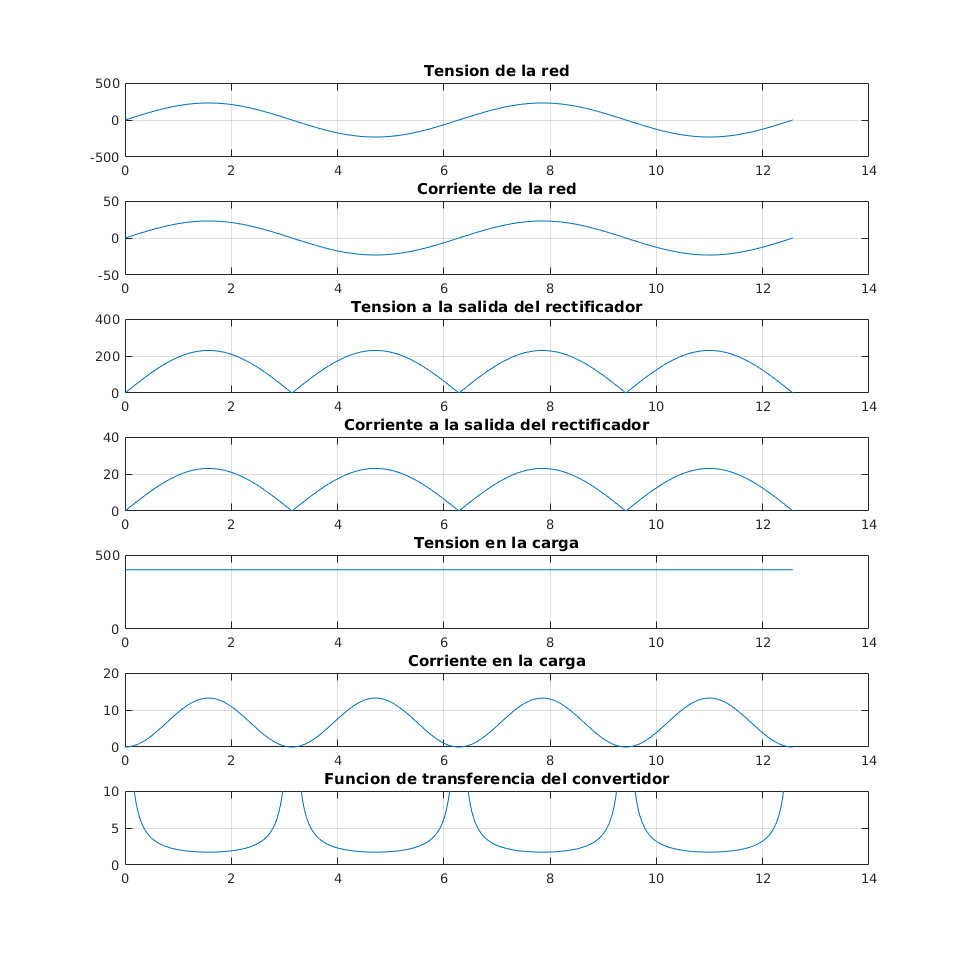 Debido a que se conserva la potencia que recibe la carga emulada \(R_e\), la corriente en la carga \(R\) es:
Debido a que se conserva la potencia que recibe la carga emulada \(R_e\), la corriente en la carga \(R\) es:
\[i_o = \frac{v_r(t)\cdot i_r(t)}{V_o} = \frac{V^2_m}{2\cdot V_o \cdot R_e}\left(1-cos(2\omega t) \right) \]
Por tanto, la corriente de salida tiene una componente DC de valor \(\frac{V^2_m}{2\cdot V_o \cdot R_e}\) y una componente frecuencial a \(2f_{red}\) que puede ser filtrado.
Sin embargo, como se puede observar, en los puntos en los que la tensión \(V_r\) es 0, en \(0, \pi, 2\pi\), el convertidor debe ser capaz de obtener \(V_{DC}\) a la salida. Esto implica que la función de transferencia tienda a infinito (lo que en la práctica no es posible). Debido a esta limitación, se producirá un error en la forma de onda de la corriente absorbida por el DC/DC en los pasos por 0, teniendo una distorsión armónica diferente de 0 pero muy reducida.
A la hora de elegir el tipo de convertidor DC/DC, se tiene que tener en cuenta que este debe ser capaz de trabajar en todo el rango de M. Por ejemplo, un convertidor buck tiene una relación de transformación \(M\leq 1 \), por lo que en aquellos puntos en los que la tensión de entrada del convertidor sea menor que la tensión de salida objetivo, se pierde el control del convertidor y este no va a ser capaz de trabajar en esta zona.
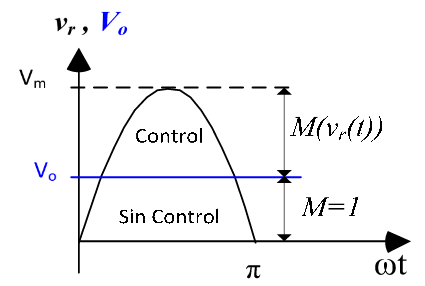 Lo más apropiado entonces sería utilizar un convertidor buck-boost. Sin embargo, debido a la disposición de la bobina en esta configuración (en derivación) no es posible hacer un control en corriente. El control en corriente es interesante debido a que es la magnitud que realmente queremos modelar. Por tanto teniendo en cuenta esta limitación, esta configuración no se suele utilizar.
Lo más apropiado entonces sería utilizar un convertidor buck-boost. Sin embargo, debido a la disposición de la bobina en esta configuración (en derivación) no es posible hacer un control en corriente. El control en corriente es interesante debido a que es la magnitud que realmente queremos modelar. Por tanto teniendo en cuenta esta limitación, esta configuración no se suele utilizar.
También se pierde el control del convertidor como ya se ha dicho en los puntos de la tensión de entrada \(V_r\) cercanos a 0, ya que el ciclo de trabajo en estos puntos tiende a 1 aunque no hay tensión. El convertidor boost (\(M\geq 1\)) es el más utilizado en pre-reguladores HPF monofásicos.
Pre-regulador monofásico mediante convertidor boost
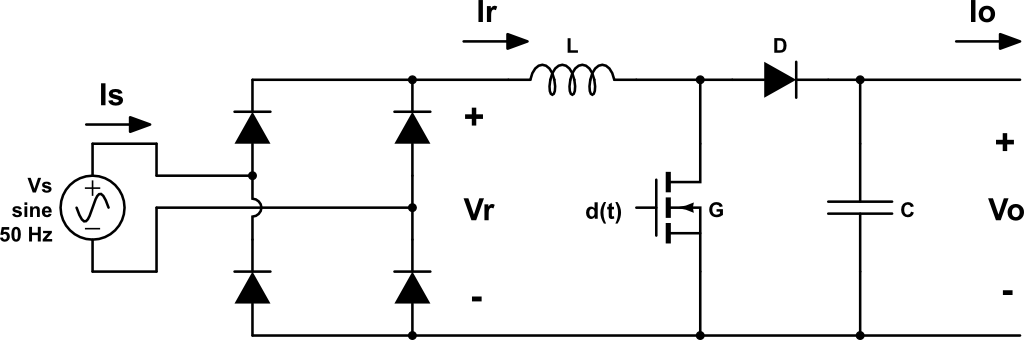
El pre-regulador monofásico mediante convertidor boost es el que se muestra en la figura. Idealmente, el convertidor boost puede producir cualquier ratio de conversión que esté entre 1 e infinito. La relación de transformación de este convertidor es:
\[ M(d(t)) = \frac{V_o}{V_r} = \frac{1}{1-d(t)}\]
Despejando el ciclo de trabajo:
\[ d(t) = 1-\frac{v_r(t)}{V_o}\]
donde \(V_o\) es la tensión continua que se quiere conseguir a la salida y \(v_r(t)\) es la tensión a la salida del rectificador. Sin embargo, esta expresión solo es cierta cuando la corriente en la bobina está en conducción continua.
Para garantizar la conducción continua, el rizado de corriente en la bobina debe ser menor o igual que 2 veces la corriente media en la bobina:
\[ \Delta i_L \leq 2i_{L(AV)}\]
Donde hay que tener en cuenta que la corriente media que pasa por la bobina es la corriente media que el rectificador toma de la red (\(i_{L(AV)} = i_{r(AV)}\)). Vamos a calcular primero el valor de la corriente media en la bobina (o lo que es lo mismo, de la red). La corriente de salida está relacionada con la corriente de entrada mediante la siguiente expresión:
\[ \frac{I_o}{I_{r~(AV)}} = 1 – D \]
Despejando \(I_{r~(AV)}\), tenemos:
\[ I_{r~(AV)} = \frac{I_o}{1 – D} = \frac{\frac{V_o}{R}}{1-D} = \frac{V_o}{R\left(1-D\right)}~~~(1)\]
Sin embargo, esta ecuación no nos relaciona la corriente media de salida con la resistencia emulada \(R_e\). Para poder relacionarlas, sabemos que la función de transferencia de la tensión es:
\[ \frac{V_o}{V_{r~rms}} = \frac{1}{1-D} \]
\[V_o = \frac{V_{r~rms}}{1-D}\]
Como R es la relación entre la tensión de salida y la corriente de salida:
\[ R = \frac{V_o}{I_o} = \frac{V_{r~rms}}{I_{r~rms}} \frac{1}{\left(1-D\right)^2} = \frac{R_e}{ \left( 1-D\right)^2 } \]
Donde \(R_e\) es la resistencia equivalente vista desde la salida del rectificador.
Retomando la expresión de la corriente de entrada (1):
\[ I_{r~(AV)} = \frac{V_o}{R\left(1-D\right)} = \frac{V_o}{R_e}\left(1-D\right) = \frac{V_{r~rsm}}{R_e}\]
\[ i_{r~(AV)} = \frac{v_r(t)}{R_e}\]
Por lo que ya tenemos la ecuación que relaciona la corriente media que proporciona la red con la resistencia emulada \(R_e\).
Ahora vamos a calcular la otra parte de la inecuación y tener las condiciones que aseguran que el convertidor trabaja en conducción continua, que interesa como hemos visto para que la relación de transformación sea válida. El rizado de corriente en el convertidor boost es:
\[ \Delta i_r = \frac{v_r(t)}{L}d(t)T_{s}\]
Por tanto, como habíamos dicho y siendo \(i_L = i_r\), para garantizar conducción continua:
\[ \Delta i_L \leq 2i_{L(AV)}\]
\[ \frac{v_r(t)}{L}d(t)T_{s} < 2\frac{v_r(t)}{R_e} \]
Despejando \(R_e\):
\[ R_e < \frac{2L}{d(t)T_{s}} \]
Despejando \(d(t)\):
\[ d(t)< \frac{2L}{R_e T_{s}} \]
Si se cumplen estas ecuaciones, el convertidor estará en conducción continua y la relación de transformación que nos interesa se cumplirá. Sin embargo, estas últimas ecuaciones las podemos reescribir de la siguiente manera:
\[ R_e < \frac{2L}{\left(1-\frac{v_r(t)}{V_o}\right)T_{s}} \]
Como \(v_r(t) = V_M \left| \sin(\omega t) \right|\), es decir que \(0\leq V_r \leq V_M\), el valor máximo que puede tener \(R_e\) sea da cuando \( \frac{2L}{\left(1-\frac{v_r(t)}{V_o}\right)T_{s}}\) sea mínimo. Y esto sucede cuando el denominador es máximo. Dicho de otro modo, el máximo valor que puede tomar \(R_e\) se da cuando \(v_r(t) = 0\). Por tanto, el máximo valor de \(R_e\) que hace que el convertidor esté trabajando en modo corriente continua es:
\[ R_e < \frac{2L}{T_s} \]
El valor de \(R_e\) nos va a servir para diseñar la bobina del convertidor. Sabiendo que:
\[ R_e = \frac{V^2_{r(rms)}}{P_o} = \frac{V^2_m}{2P_o} \]
Entonces, sustituyendo:
\[ \frac{V^2_m}{2P} < \frac{2L}{T_s} \Rightarrow L > \frac{V^2_m \cdot T_s}{4P} \]
Por tanto, este será el mínimo valor de inductancia que conseguirá que el convertidor esté trabajando en modo conducción continua.
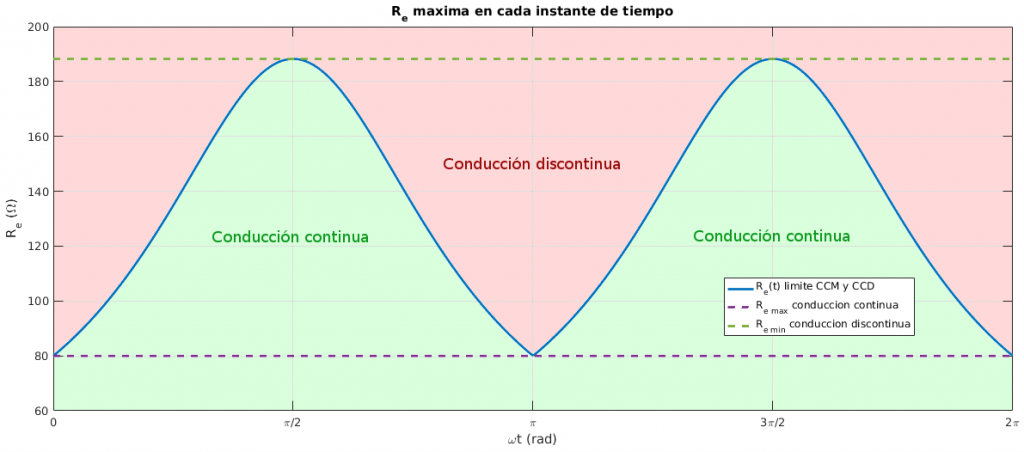
Sin embargo, el valor de la inductancia de la bobina no será cualquier valor por debajo del mínimo. De hecho, en muchos casos tendremos impuesto un rizado máximo de corriente en la bobina. En ese caso, la expresión del rizado de la corriente en la bobina será el que limitará el mínimo valor de la inductancia. De la ecuación del rizado de la corriente en el convertidor boost:
\[ \Delta I_L = \frac{V_{r~rms}}{L}DT_s = \left\{ \frac{V_o}{V_{r~rms}} = \frac{1}{1-D} \right\} = \frac{V_o}{L} D \left(1-D\right)T_s \]
Despejando L:
\[ L = \frac{V_o}{\Delta I_L} D \left(1-D\right)T_s \]
El valor del ciclo de trabajo D que maximiza la ecuación es \(D = 0.5\).
\[ \left. D \cdot \left(1-D\right)\right|_{D=0.5} = 0.25 = \frac{1}{4} \]
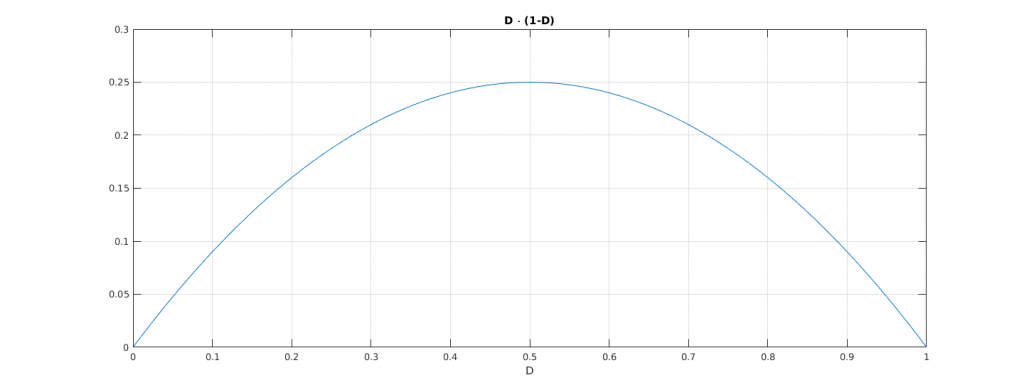 Teniendo este valor en cuenta, para cumplir que el rizado de corriente sea menor que el exigido:
Teniendo este valor en cuenta, para cumplir que el rizado de corriente sea menor que el exigido:
\[ L > \frac{V_o}{4\Delta I_L} T_s \]
De esta manera quedaría totalmente diseñada la bobina.
El último componente que queda por determinar es el condensador. La función del condensador es la de proporcionar potencia a la salida cuando la potencia suministrada por la red es 0. Debido a que la corriente está en fase con la tensión y tienen la misma forma de onda, en \(\pi\) y \(2\pi\) la potencia es que entrega la red es 0. Sin embargo, la potencia que queremos entregar a la carga es constante. Para arreglar esta situación, el condensador se cargará en un cuarto de periodo almacenando energía y se descargará en el otro cuarto de periodo. Esta situación se muestra en la siguiente figura:
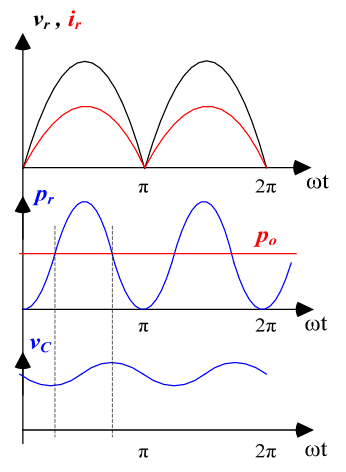 La potencia que suministra la red es:
La potencia que suministra la red es:
\[ p_r(t) = v_r(t) \cdot i_r(t) = \frac{V^2_m}{R_e}\sin^2(\omega t) = \frac{V^2_m}{2R_e}\left[1-\cos\left(2\omega t\right)\right]\]
La potencia media entregada a la carga, será la potencia media suministrada por la red:
\[ P_{r(AV)} = P_o = \frac{V^2_m}{2 R_e}\]
La potencia suministrada por el condensador debe ser la diferencia entre la que pide la carga y la que entrega la red:
\[ p_c(t) = p_r(t) – p_o(t) \]
La energía almacenada en un condensador es:
\[ E_c = \frac{1}{2} C V^2_c \]
Por tanto, la potencia del condensador será:
\[ p_c(t) = \frac{dE(t)}{dt} = \frac{d}{dt}\left[\frac{1}{2} C v^2_c(t)\right] \]