¿Qué podemos hacer si queremos obtener una tensión de 50V a partir de una de 100V? Quizá una de las respuestas más inmediatas sea utilizar un divisor resistivo, pero es evidente que la eficiencia del sistema es más bien escasa. ¿Y si queremos obtener una tensión de 100V a partir de una de 50V? Para hacer este tipo de ajustes, se utilizan fuentes conmutadas. Estas son las responsables de que actualmente los cargadores de móvil (por poner un ejemplo) sean tan pequeños, en comparación a los de hace unos años, que tenían un peso y unas dimensiones considerables.
Las fuentes conmutadas, a su vez, utilizan el principio de las bobinas a no poder cambiar bruscamente su corriente. De esta manera se puede conseguir aumentar o disminuir una tensión con una eficiencia superior al 90%. Existen 3 tipos de conversores DC-DC:
- Buck: son aquellos que son capaces de reducir una tensión de entrada. Si aplicamos 100V a la entrada de un conversor, podemos conseguir una tensión menor sin sufrir las pérdidas inherentes del divisor resistivo.
- Boost: son capaces de generar tensiones superiores a las de entrada. De esta manera podriamos pasar una señal de 3V a 5V sin necesidad de fuentes de alimentación adicionales.
- Buck-boost: el nivel de conversión de estos es variable y pueden conseguir tanto ganancias menores que uno como superiores a la unidad.
Un ejemplo un poco más complejo de conversor buck-boost habitual es el conversor Ćuk (pronunciado como Chook). Consta de 2 condensadores y 2 inductores, un transistor y un diodo. La principal ventaja respecto a los buck-boost más sencillos es que el rizado de tensión a la salida es menor.
La disposición del circuito es la siguiente:
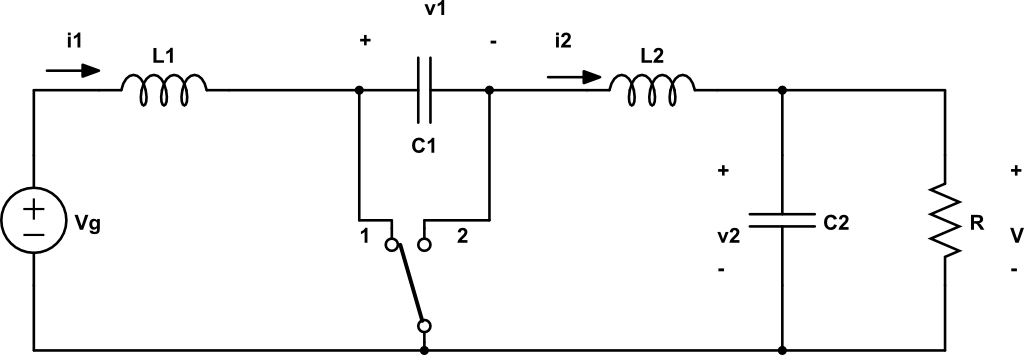
Ganancia
Para analizar circuitos de potencia, hay que fijarse en los parámetros que pueden cambiar bruscamente para cada componente: la tensión en las bobinas, la corriente en los condensadores.
Con el interruptor en la posición 1:
\[v_{L_1} = V_g\]
\[v_{L_2} = -V_1 – V_2\]
\[i_{C_1} = i_2\]
\[i_{C_2} = i_2 – \frac{V_2}{R}\]
Con el interruptor en la posición 2:
\[v_{L_1} = V_g – V_2\]
\[v_{L_2} = – V_2\]
\[i_{C_1} = i_1\]
\[i_{C_2} = i_2 – \frac{V_2}{R}\]
Por tanto, la forma de las señales en el conversor Ćuk son:
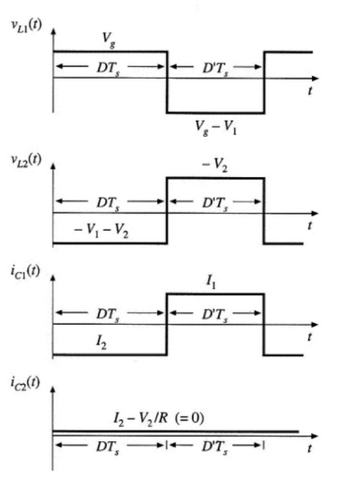
En régimen estacionario, el valor medio de todas las tensiones y corrientes debe ser cero (de lo contrario indicaría que no estamos en regimen estacionario). Por tanto:
\[v_{L_1} = V_g DT_s +\left(V_g-V_1\right)D’T_s = 0\]
\[v_{L_2} = \left(-V_1 – V_2\right) DT_s+ V_2 D’T_s = 0\]
\[i_{C_1} = I_2 DT_s +I_1 D’T_s = 0\]
\[i_{C_2} = i_2 + \frac{V_2}{R} = 0\]
A la hora de definir las ecuaciones es importante tener en cuenta si se toma el valor sin modificar el signo o si por lo contrario se calcula a partir del area. En caso de coger el valor sin modificar el signo, la suma de ambos debe ser 0. Sin embargo, si se escoge el area, la resta de las dos areas debe ser 0. En este caso he optado por la forma más genérica que es tomar los valores conforme están, sin cambiar signos. Tened cuidado en este paso porque si se mezclan ambos procedimientos simplemente las expresiones no cuadran.
Resolviendo el sistema de ecuaciones, obtenemos:
\[V_1 = \frac{V_g}{D’}\]
\[V_2 =-\frac{D}{D’}V_g\]
\[I_1 = \left(\frac{D}{D’}\right)^2V_g\]
\[I_2 = -\frac{D}{D’}\frac{V_g}{R}\]
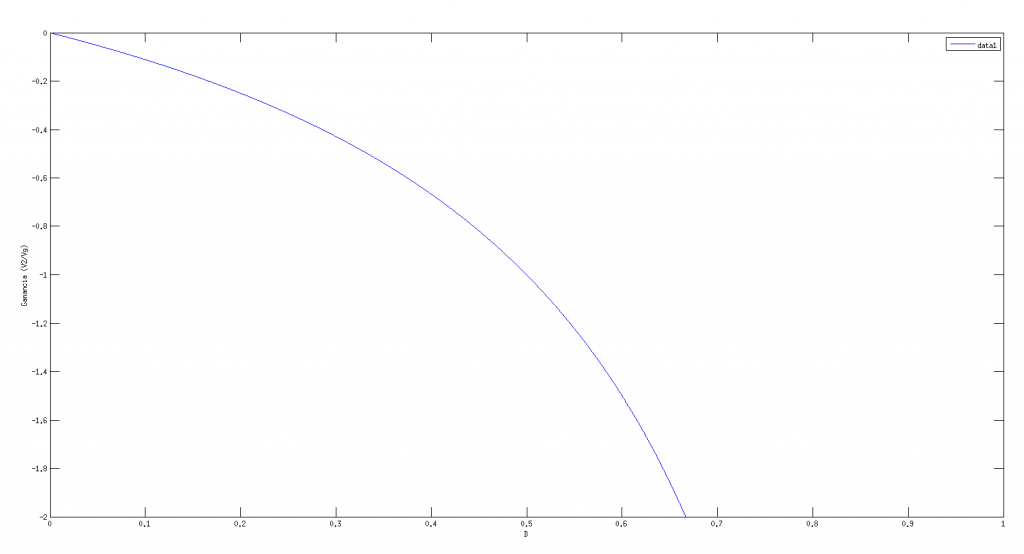
Como podemos observar, la ganancia del sistema es \(\frac{V_2}{V_g} = \frac{D}{1-D}\). Si lo reprensentamos en función de D, vemos perfectamente que el conversor pertenece a la clase buck-boost, ya que teóricamente es capaz de tener cualquier ganancia entre 0 y 1.
Como se puede esperar de una función del tipo \(\frac{x}{1-x}\), cuando nos aproximamos al 1 tiende a infinito.
Rizado de tensión y corriente
Por último falta calcular la magnitud del rizado de las tensiones y corrientes. Ello nos ayudará a escoger los valores de inductancia y de capacidad. Para calcularlos simplemente utilizamos la propiedad de corriente en un inductor y de tensión en un condensador:
\[\frac{di\left(t\right)}{dt} = \frac{v\left(t\right)}{L}\]
\[\frac{dv\left(t\right)}{dt} = \frac{i\left(t\right)}{C}\]
Como conocemos estos valores, podemos calcular la corriente en las bobinas y la tensión en el condensador fácilmente.
Durante el primer subintervalo, los valores son:
\[\frac{di_1\left(t\right)}{dt} = \frac{v_1\left(t\right)}{L} = \frac{V_g}{L_1}\]
\[\frac{di_2\left(t\right)}{dt} = \frac{v_2\left(t\right)}{L} = \frac{-V_1-V_2}{L_2}\]
\[\frac{dv_1\left(t\right)}{dt} = \frac{i_{c_1}\left(t\right)}{L} = \frac{I_2}{C_1}\]
Sabiendo la derivada, sabemos la pendiente, por lo que tendrían un aspecto parecido al siguiente:
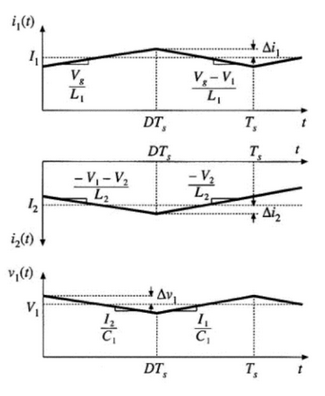
Sabiendo la pendiente y cuánto tiempo dura, podemos calcular la variación máxima. Como la forma del rizado debe ser simétrica, podemos calcularlo como la pendiente (V/s o A/s) por el tiempo DTs (s). Como queremos el rizado de pico y no el rizado pico a pico, tenemos que dividir por 2. Luego reordenando términos para dejarlo en función de los parámetros conocidos:
\[\Delta i_1 = \frac{V_g D T_s}{2L_1}\]
\[\Delta i_2 = \frac{-V_1-V_2}{2L_2}\cdot D T_s = \frac{V_g D T_s}{2L_2}\]
\[\Delta v_1 = \frac{I_2}{2C_1}\cdot D T_s = \frac{V_g D^2 T_s}{2 D’ R C_1}\]
Como vemos, falta el rizado más importante, que es el rizado de la tensión de salida. Sin embargo no podemos aplicar el mismo procedimiento para calcularlo, ya que el resultado es que el rizado es 0. Esto ocurre en todos los conversores con dos polos en la función de transferencia del filtro paso bajo. En estos casos, la única componente que entrega corriente al condensador viene de la bobina. Por tanto vamos a estudiar con detenimiento como es la corriente del condensador sabiendo como es la de la bobina L2.
La forma del rizado de corriente será el mismo que el del inductor. Sin embargo, no tendrá componente continua. ¿Por qué? Porque el condensador está en paralelo con una resistencia, con lo que si suponemos que el condensador está bien diseñado como para tener una impedancia mucho mayor a frecuencias bajas, toda la componente continua la absorbería la resistencia y el condensador se quedaría con el rizado. Tiene sentido, ¿no?
Ahora bien, para calcular la tensión del condensador a partir de su corriente, solo tenemos que integrar.
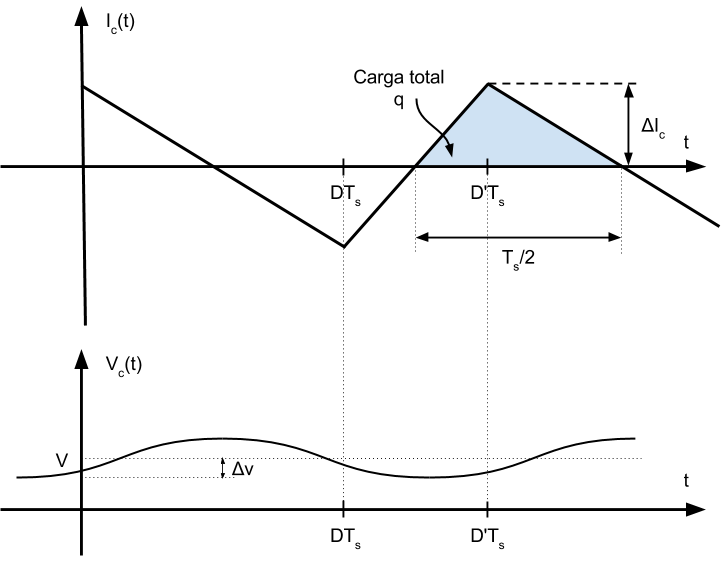
Cuando la corriente en el condensador es positiva, la carga que almacena aumenta. Esta carga la podemos expresar de dos manera: utilizando la corriente y utilizando el valor de tensión:
\[q = C \left( 2 \Delta v \right)\]
\[q = \frac{1}{2} \Delta i_L \cdot \frac{T_s}{2}\]
Igualando las ecuaciones, finalmente conseguimos una expresión para el rizado de la tensión de salida:
\[\Delta v = \frac{\Delta i_L T_s}{8 C}\]
Y esta es toda la información que necesitamos para poder dimensionar un convertidor DC-DC buck-boost Ćuk. Sabiendo cuál es rizado máximo que queremos a la salida, podemos obtener todos los valores. El procedimiento que se ha aplicado para calcular los parámetros es perfectamente extrapolable a cualquier otro convertidor, así que solo necesitaréis particularizar las formas de tensión y corriente para conseguir analizar completamente un de estos circuitos.