The fixed point representation consists of the representation of decimal numbers using a binary coding scheme that can’t model exactly all decimal numbers. Before getting into details, we are going to have a brief overview on different binary encondings schemes that there are.
Binary encoding using fixed point
\[ (10010)_2 = 1 \cdot 2^4 + 0 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1 + 0 \cdot 2^0 = 18 \]Binary encoding using floating point
The number value doesn’t depend on the bit position. The binary number is split into 3 different parts: sign, mantissa and exponent
The value is computed as:
\[ \text{Value} = S \cdot M \cdot 2^{E-cte} \]
The floating point encoding provides a much greater dynamic range than the fixed point encoding. Furthermore, the resolution can be variable. Nevertheless, performing the addition operation using floating point enconding is more complex.
Fixed point encoding for unsigned integers (positive)
The encoding for N bits unsigned numbers has a range \(\left[0, 2^N -1 \right]\). In this case, the resolution is 1.
In order to compute the value of a binary number:
\[ X = \sum_{i=0}^{N-1} x_i 2^i\]
Fixed point enconding for integers with sign
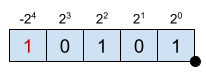
The enconding for N bits numbers with sign can be done using 2’s complement. In this encoding every bit has a weight, just as in the unsigned integers. The particularity here is that the most significant bit (MSB) has a negative sign and the corresponding power of 2 weight given by its position.
As it can be seen, the MSB has a weight of \(2^{-4}\) and a negative sign.
El 2’s complement range is \(\left[-2^{N-1}, 2^{N-1}-1 \right] \) and the resolution 1.
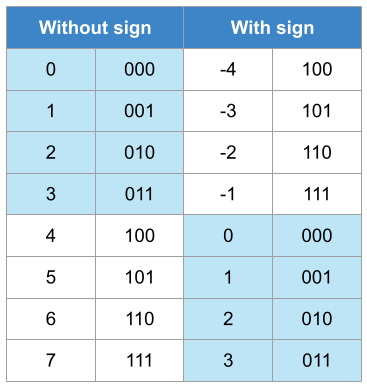
Comparison between numbers with sign and 2’s complement
The table illustrated the representation with and without sign and its equivalence to the decimal format. In this case, N = 3 since only 3 bits are used to represent all the numbers. The range for the representation without sign is [0, 7] whereas in the case of the representation with sign is [-4, 3].
The values that are lower than \(2^{N-1} = 2^{3-1} = 2^2 = 4\) have their direct equivalency in both encodings (blue background), i.e., both are presented as \((011)_2\)
In the case of values without sign greater than \(2^{N-1}\), they should be read as:
\[ \text{Signed} = \text{Unsigned} – 2^N \]
For instance, 6 represented as unsigned is \((110)_2\). However, \((110)_2\) interpreted as a 2’s complement number is:
\[ \text{Signed} = 6 – 2^3 = 6 – 8 = -2\]
Therefore:
\[ S = \left\{\begin{matrix}
U; & U < 2^{N-1} \\
U – 2^N ;& U \geq 2^{N-1}
\end{matrix}\right.\]
Encoding positive real numbers using fixed point
Decimal numbers can also be represented using fixed point encoding. Nonetheless, the value accuracy will depend on the number of bits used and the point position.
\[X_Q = 2^{2} + 2^0 +2^{-2} = 5.25 \]
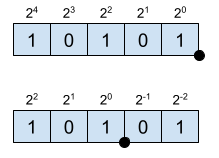
The position of the point is imaginary since it not specified internally in any way. From the position of the point towards the left, the numbers represent positive powers of 2. Towards the right, negative powers of 2. The resolution of this enconding is given by the LSB.
\[ X = \left(\sum_{i=0}^{N-1} x_i 2^i \right) \cdot 2^{-b} \]
The notation used to describe this enconding is \([N, b]\), where \(N\) is the total number of bits and \(b\) is the number of fractional bits. For example, \([6,3]\) means 6 bits in total 3 of which are fractional. In this case, the resolution is \(2^{-3} = 0.125\).
Enconding real numbers using fixed point in 2’s complement
When representing real numbers with sign using 2’s complement, the range of the numbers is \([-2^{N-1}\cdot Q, (2^{N-1}-1) \cdot Q]\), where N is the total number of bits and Q the resolution, which is \(Q = 2^{-b}\).
\[ X = \left(-x_{N-1} 2^{N-1} + \sum_{i=0}^{N-2} x_i 2^i \right) \cdot 2^{-b} \]
- Example 1:
- N = 6, b = 3, format [6,3].
- Range: \(\left[2^{6-1}\cdot 2^{-3}, (2^{6-1}-1)\cdot 2^{-3} \right] = \left[-4, 3.875\right] \).
- Resolution: \(2^{-3} = 0.125\).
- Example 2:
- N = 5, b = 2, format [5,2].
- Range: \(\left[2^{5-1}\cdot 2^{-2}, (2^{5-1}-1)\cdot 2^{-2} \right] = \left[-4, 3.75\right] \).
- Resolution: \(2^{-2} = 0.25\)
Encoding dynamic range
The dynamic range of an encoding is determined by the amount of numbers used to encode a range of number. For instance, in the fixed point encoding without sign, the range is \([0, \left(2^{N}-1\right)\cdot Q]\) and the resolution \(Q=2^{-b}\).
The dynamic range is the relationship between the maximum encoding difference \([-2^{N-1}, 2^{N-1} 1]\) and the encoding resolution.
\[ DR = \frac{N_{max}-N_{min}}{Q} = \frac{ \left(2^{N}-1\right)-0}{Q} = 2^{N}-1 \]
In the case of the 2’s complement encoding, the range is \([-2^{N-1}, 2^{N-1}-1]\) and the resolution is again \(Q= 2^{-b}\). The dynamic range is also \(2^{N}-1\).
If this is computed in dB, defining the dynamic range as \(20\log_{10}\{·\}\), we can obtain that the dynamic range is approximately 6.02N dB. Therefore, every bit increase the encoding dynamic range in 6.02 dB.
Effects of the finite accuracy
The factor of working with encodings with finite accuracy it has effects on the signal we are working with. The effects can be of two different types:
- Decrease the number of integer bits, which reduces the range of the encoding. This can lead to misrepresent the signal using a particular encoding. For example, a sine with range [0, 8] can’t be encoded with U[4, 3] since numbers greater than \(2^{4} \cdot 2^{-3} = 2\) can’t be represented. This can have two different consequences over the signal:
- Wrap: the signal is wrapped and the higher numbers are represented near the low values of the range.
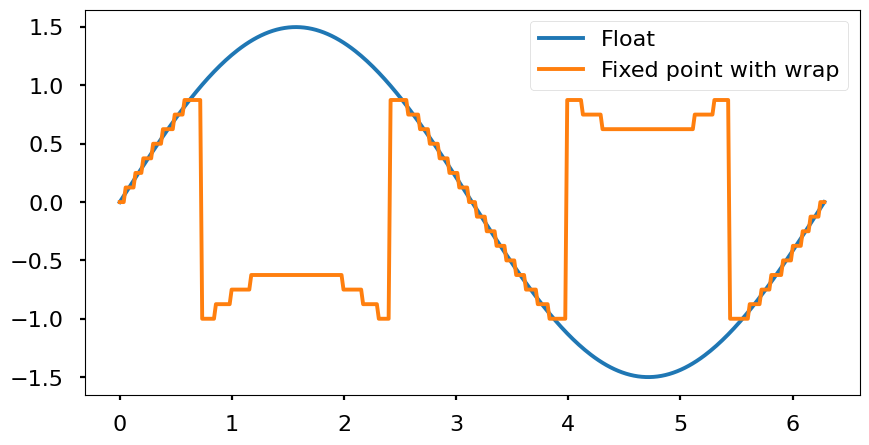Example: S[4,3], range [-1, 0.875], resolution \(2^{-3} = 0.125\). If this encoding represent a number out of the range, \(1.125 = (01.001)_2 \), we only have 1 bit to represent the integer part. Therefore, it will be cut to \((1.001)_2\) which converting this 2’s complement number to decimal it is \( \left(-2^{3} + 2^{0} \right) \cdot 2^{-3} = -0.875\)
-
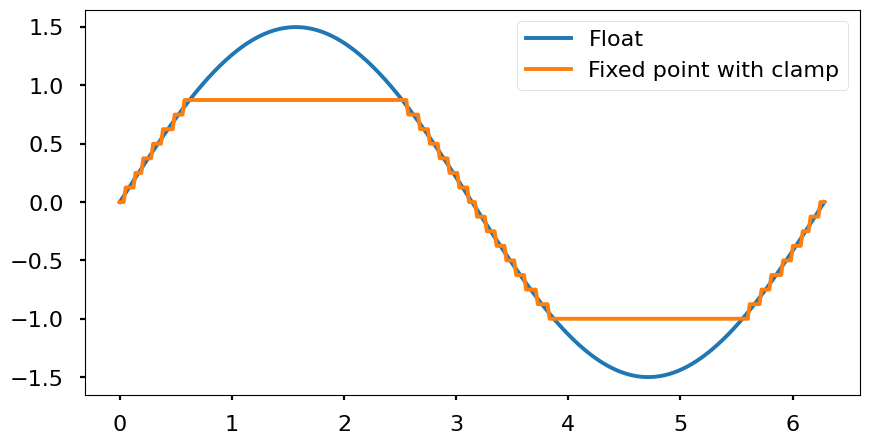
- Clamp: all numbers outside the range are «saturated» to the maximum (or minimum) value. In order to represent the campling, it is necessary to include extra logic to take these cases into account.
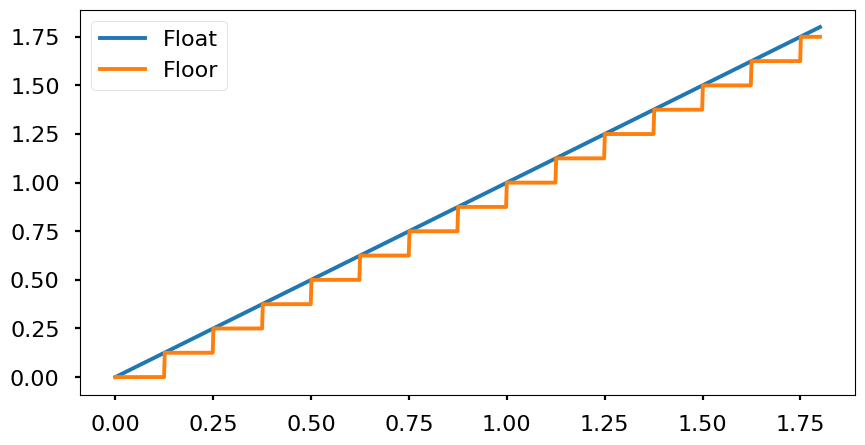
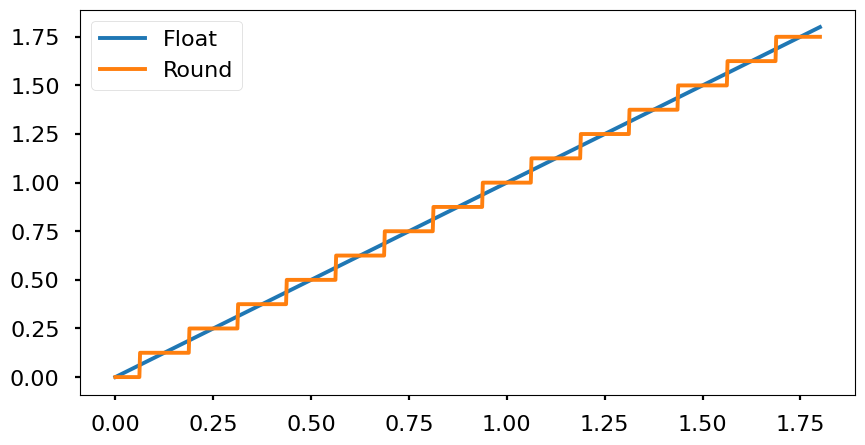
- Quantization: since all decimal numbers can’t be represented due to the finite accuracy of the encoding, all possible values will be multiples of the resolution. Every real number between two multiples of the resolution will be mapped to one of the nearest multiples. Therefore, the signal will look like a stair wave. Depending the mapping technique used (nearest, floor, ceil, etc.) the effects are different. From the frequency point of view, the quantization adds white noise that is spreaded througout all the signal band (from 0 Hz to half of the sampling frequency \(\frac{f_s}{2}\).
- Floor: «flooring» means to round to the nearest low value. This produces a maximum error of -Q and in average -Q/2. However, computationally is simple to resolve.
-
- Nearest: round to the nearest value. It rounds up if Q/2 is exceeded and down if the value is below Q/2.
Implementation of nearest and floor
In MATLAB the functions round() and floor() can be used for computing the nearest and floor integer value of a number. Therefore, if we want to round to 2 decimals the number 12.5432 what we need to do is:
- Shift two digits to the left multiplying the number by 100: 12.5432 · 100 = 1254.32
- Apply the rounding method:
floor(1254.32) = 1254 - Shift two digits to the right dividing the number by 100: 1254/100 = 12.54
In the binary encoding, the operation is the same. The only difference is that instead of using powers of 10 to shift number, we use powers of 2.
Example: round to 3 fractional bits \(1.28515625 = (01.01001001)_2 \)
- Shift 3 digits to the left multiplying by \(2^3\): \(1.28515625 \cdot 2^3 = 10.28125\)
- Apply the
floor()function.floor(10.28125) = 10 - Shift 3 digits to the right multiplying by \(2^{-3}\): \(10 \cdot 2^{-3} = 1.25 = (01.010)_2\)
Quantizing fixed point number in MATLAB
In MATLAB we can use the function quatize(q, a). It can be used to compute the quantized number with a given fixed point encoding. This function has two parameters:
- q: is the quantizer object that defines the enconding to be used. It is defined with the function
quantizer(Format, Mode, Roundmode, Overflowmode), where:- Format: [N b]
- Mode: ‘fixed’ o ‘ufixed’ for a fixed point encoding signed or unsigned.
- Roundmode: ‘floor’, ‘round’ for nearest.
- Overflowmode: ‘saturate’ or ‘wrap’
- a: number to quantify
Definition of fixed point in Simulink
In Simulink, we can use the function fixdt(Signed, WordLength, FractionLength) to the define the encoding format.
Modifying the resolution or scaling
Extending the resolution
This is the situation in which we want to represent the fractional part with more bits than in the original encoding. This operation is as straightforward padding with zeros at the right of the binary number.
Reducing the resolution
The fractional part of the number is represented with less bits than in the original encoding. Therefore, the resolution is shrinked.
Example:
\(A = 2.625 = (010.101)_2\)
\(A [6,3] \rightarrow A = A_e \cdot 2^{-3} =(010101)_2 ~~A_e = (010101)_2 21 \)
\(A’ [4,1] \rightarrow A’ = A’_e \cdot 2^{-2} =(0101)_2~~A’_e = (0101)_2 = 5 \)
This operation can be intuitively understood as changing the integer part of the number. For instance, the initial number could be interpreted as unsigned as \(A_e = 21\) because the integer part was using 6 bits in total. If we cut the total number of bits used to 4, then the unsigned value is lower than before (5). FInally, if we need to scale the number moving the «fixed point» where necessary to obtain the final value on the new encoding.
Example:
\(A’_e = floor\left(A_e \cdot 2^{-2}\right) = 5\)
In this case, we need to multiply by \(2^{-2}\) because we need to go from a resolution of \(2^{-3}\) to \(2^{-1}\). Therefore, we need to shift the point 2 positions to the right.