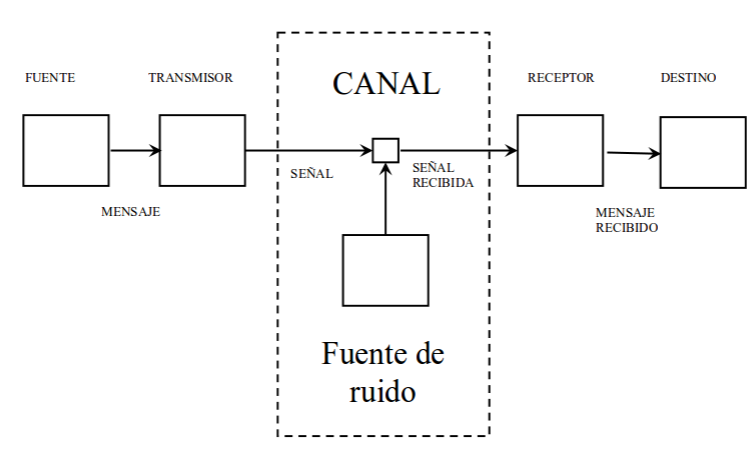
Anteriormente hemos hablado del concepto de información y de entropía en una fuente de comunicaciones, parámetros necesarios para poder modelar matemáticamente una fuente de información en comunicaciones. Toda fuente quiere enviar información a un destino, el usuario y de manera obligatoria debe utilizar un canal mediante el cual enviar esta información. En comunicaciones móviles sería el aire, en comunicaciones ópticas la fibra óptica o en comunicaciones guiadas podrían ser cables coaxiales, multifilares, etc.
Por tanto, es necesario disponer de herramientas para modelar el canal, ya que usualmente suele ser un entorno hostil en el que está presente ruido, interferencias y demás impedimentos que dificultan la comunicación. Normalmente, los terminales de comunicación se consideran perfectos (sin ruido, sin distorsión, etc.) y es en el canal en el que se tienen en cuenta todas estas no idealidades. Por tanto el canal se considera el vehículo de transmisión al que se le suman todos los fenómenos que tienden a limitar la comunicación. El hecho de que haya límites físicos para el envío de información nos lleva a la noción de capacidad del canal.
Del mismo modo que la entropía mide la cantidad de información que una fuente puede dar en un tiempo determinado, la capacidad del canal mide la cantidad de información que un canal puede transmitir por unidad de tiempo.
Teniendo en cuenta la capacidad del canal, el teorema fundamental de la teoría de la información se puede reescribir como:
\(C\) y una fuente con una tasa de entropía \(R\), si \(R \leq C\), existe una técnica de codificación tal que la salida de la fuente puede ser transmitida a lo largo del canal con una frecuencia de errores arbitrariamente pequeña a pesar de la presencia de ruido. Si \(R > C\), no es posible transmitir sin errores.
Caracterización de un canal
Un canal se caracteriza estadísticamente. La caracterización de un canal supone conocer la probabilidad de tener a su salida todos los símbolos que la fuente puede transmitir.

En un canal discreto sin memoria (los símbolos son independientes), la función de verosimilitud es la que caracteriza el canal
\[ P\left(Y | X \right) = \{ P\left(y_j | x_i \right) \} \]
La ecuación nos dice cuál es la probabilidad de que a la salida del canal haya el símbolo Y habiendo transmitido X, pues el receptor debe adivinar cuál ha sido X (el valor realmente enviado por la fuente) habiendo recibido el símbolo Y.
Otras definiciones que también se emplean son:
\[ P\left(X = x_i\right) = P\left( x_i\right)\]
La probabilidad a priori es propia de la fuente y nos dice cómo de probable es que un símbolo (\(x_i\)) se transmita.
\[ P\left(X | Y \right) = \{ P\left(x_i | y_j \right) \} \]
\[ P\left(X = x_i, Y = y_j \right) = P \left( x_i | y_j \right) P \left(y_j \right) = P \left(y_j | x_i \right) P \left( x_i \right)\]
La ecuación quiere decir que la probabilidad de enviar \(x_i\) y recibir \(y_j\) es la probabilidad a posteriori (enviar \(x_i\) habiendo recibido \(y_j\)) por la probabilidad de recibir \(y_j\) o del mismo modo, es la función de verosimilitud (probabilidad de recibir \(y_j\) habiendo enviado \(x_i\)) multiplicado por la probabilidad de enviar \(x_i\).
Dicho de otro modo más, ¿cuál es la probabilidad de tener \(x_i\) a la entrada e \(y_j\) a la salida? Si \(x_i\) fuese independiente de \(y_j\), la probabilidad debería ser \(P\left(x_i\right) \cdot P\left(y_j \right)\). Sin embargo, si tuviésemos un canal en el que su salida fuese independiente de su entrada sería una auténtica basura. Por eso es necesario tomar las probabilidades condicionadas. Probabilidad de tener \(y_j\) habiendo enviado \(x_i\) por la probabilidad de enviar \(x_i\).
Resumen
\(P\left( x_i\right)\) es la probabilidad de que la fuente seleccione el símbolo \(x_i\) para transmitir. (Probabilidad a priori)
\(P\left( y_j \right)\) es la probabilidad de que el símbolo \(y_j\) haya sido recibido en el destino (al otro lado del canal).
\(P\left( x_i, y_j \right)\) es la probabilidad conjunta de que \(x_i\) sea transmitido y \(y_j\) sea recibido.
\(P\left( x_i | y_j \right)\) es la probabilidad condicional de que \(x_i\) sea transmitido dado que \(y_j\) haya sido recibido. (Probabilidad a posteriori)
\(P\left( y_j | x_i \right)\) es la probabilidad condicional de que \(y_j\) sea recibido dado que \(x_i\) haya sido transmitido. Esta probabilidad incluye las probabilidades de error de símbolo. (Función de verosimilitud)
Ejemplo de canal discreto sín memoria
Canal binario borrador \(BEC(\epsilon)\)
Información mutua \(I\left(X, Y \right)\)
En el ejemplo de arriba, tenemos una fuente con dos símbolos y un destino con tres símbolos. Si el sistema está diseñado para entregar \(y_j = y_1\) cuando \(x_i = x_1\) y \(y_j = y_2\) cuando \(x_i = x_2\), entonces la probabilidad de error de símbolo viene dada por \(P\left( y_j | x_i \right)\) para \(j \neq i\).
Una descripción cuantitativa de la información transferida en el canal es mediante la información mutua.
\[I\left(x_i, y_j \right) = \log_2{\frac{P\left( x_i | y_j \right)}{P\left( x_i \right)}}~~~bits\]
La información mutua mide la cantidad de información transferida cuando \(x_i\) es transmitido y \(y_j\) es recibido.
Rango de la información mutua
El máximo se consigue en el caso de tener un canal ideal sin ruido. Es decir, cuando se recibe \(y_j\) es porque se ha enviado \(x_i\). Por tanto \(P \left( x_i | y_j \right) = 1\) y \(I\left(x_i, y_j \right) = \log_2{\frac{P\left( x_i | y_j \right)}{P\left( x_i \right)}} = \log_2{\frac{1}{P\left(x_i\right)}} = I\left(x_i \right)\), en el que la información transmitida es la de \(x_i\).
El mínimo se da cuando el ruido del canal es tan grande que la salida del canal es independiente de la entrada, por lo que \(P \left( x_i | y_j \right) = P\left( x_i \right)\). En este caso\(I\left(x_i, y_j \right) = \log_2{\frac{P\left( x_i | y_j \right)}{P\left( x_i \right)}} = \log_2{\frac{P\left(x_i\right)}{P\left(x_i\right)}} = 0\)
\[0 \leq I\left(x_i, y_j\right) \leq I\left( x_i \right)\]
En la mayoría de los casos, los canales estan entre estos dos extremos. Para analizar el caso general, se define la información mutua media:
\[I\left(X, Y \right) = \sum_{i=1}^{N}\sum_{j=1}^{M} P\left(x_i, y_j\right) I\left( x_i, y_j\right)\]
\[ =\sum_{i=1}^{N}\sum_{j=1}^{M} P\left(x_i, y_j\right) \log_2{\frac{P\left( x_i | y_j \right)}{P\left( x_i \right)}}~~~bits/simbolo\]
\(I\left(X, Y \right)\) representa la cantidad información media ganada por símbolo recibido, que debe diferenciarse de la información media por símbolo de la fuente representado por \(H\left(X\right)\)
Equivocación o entropía condicional
Utilizando relaciones de probabilidad se puede llegar a expresiones equivalentes de la información mutua.
\[P\left(x_i, y_j \right) = P\left(x_i | y_j \right)P\left(y_j \right) = P\left( x_i | y_j \right)P\left( x_i \right)\]
\[P\left( x_i \right) = \sum_{j=1}^{N} P\left( x_i, y_j \right)~~~~P\left( y_j \right) = \sum_{i=1}^{N} P\left( x_i, y_j \right)\]
\[\log{\frac{a}{b}} = \log{\frac{1}{b}} – \log{\frac{1}{a}}\]
Si empleamos estas relaciones en , llegamos a:
\[I\left(X, Y\right) = \sum_{i=1}^{N}\sum_{j=1}^{M} P\left(x_i, y_j \right) \log_{2}{\frac{1}{P\left(x_i \right)}}\\-\sum_{i=1}^{N}\sum_{j=1}^{M}P\left(x_i, y_j \right)\log_{2}{\frac{1}{P\left(x_i | y_j\right)}}\]
De manera que el primer término se simplifica de la siguiente manera:
\[\sum_{i=1}^{N}\left[ \sum_{j=1}^{M} P\left( x_i, y_j \right)\right] \log_{2}\frac{1}{P\left(x_i \right)} = \sum_{i=1}^{N} P\left(x_i \right) \log_{2}\frac{1}{P\left(x_i \right)} = H\left(X \right)\]
Por lo tanto,
\[I\left(X, Y\right)= H\left(X\right)-H\left(X|Y\right)\]
En donde \(H\left(X|Y\right)\) es la equivocación o entropia condicionada, que representa la información perdida en el canal ruidoso.
La ecuación dice que la información media transferida por símbolo es la misma que la entropía de la fuente menos la equivocación.
Volviendo a la ecuación , debido a que \(P\left(x_i | y_j \right)P\left(y_j \right) = P\left( x_i | y_j \right)P\left( x_i \right)\), se demuestra que \(I\left(X, Y\right) = I \left(Y, X\right)\), y que por tanto,
\[I\left(X, Y\right)= H\left(Y\right)-H\left(Y|X\right)\]
En la ecuación se dice que la información transferida es igual a la entropia del destino \(H\left(Y\right)\) menos la entropía del ruido \(H\left(Y|X\right)\) añadido por el canal. La interpretación de \(H\left(Y|X\right)\) como entropía de ruido sigue la observación anterior de que \(P \left( y_j | x_i \right)\) incluye las probabilidades de error de símbolo.

