Principios de magnetismo
Ley de Ampere: \( \int{H dl} = \sum{i} \)
Fuerza electromotriz: \(\epsilon = N \cdot i = l_m H \)
Ley de Faraday: en una espira se induce un flujo magnético contrario a la variación del flujo magnético que la atraviesa. Este flujo magnético opuesto induce una tensión \( v = – N \frac{d\phi}{dt} \)
En un material magnético, la fuerza electromotriz inducida depende del flujo que atraviesa el material magnético (\(\phi\)) y de su reluctancia (\(\mathfrak{R}\)), siendo la reluctancia la oposición al paso de flujo magnético.
\[ \epsilon = \phi \cdot \mathfrak{R} \]
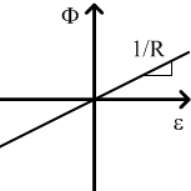
La reluctancia de un núcleo magnético depende de la longitud efectiva (cuanto más largo, más reluctancia), de su sección (cuanta más sección, menos reluctancia) y de su permeabilidad magnética (cuanto más conductivo, menos reluctancia). De esta manera podemos definir la reluctancia como:
\[ \mathfrak{R} = \frac{1}{\mu}\frac{l}{A} \]
De la misma manera que en un material eléctrico podemos definir la densidad de corriente como la corriente que pasa por un conductor por metro cuadrado (\( J = \sigma \cdot E \)), en un material magnético podemos definir la densidad de flujo magnético \( B = \mu \cdot H\), donde \(\mu\) es la permeabilidad magnética, definida como la capacidad de un material o medio para atraer y hacer pasar a través de él campos magnéticos. La densidad de flujo magnético se mide en Teslas (T).
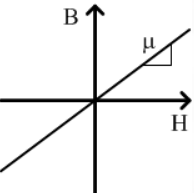
Otro parámetro a tener en cuenta es el factor de inductancia \(A_L\). Tiene unidades de Henrios (H) y es la inversa de la reluctancia (\(\mathfrak{R}\)).
\[ A_L= \frac{1}{\mathfrak{R}} = \frac{\mu A}{l} \]