Puede ser bastante interesante saber cómo poder poder representar gráficamente el espectro de frecuencia un archivo de audio con MATLAB.
Para transformar una función del dominio temporal al frecuencial, es necesario hacer la transformada de Fourier de dicha función. En el caso de una señal contínua la transformada recibe el nombre de Transformada de Fourier mientras que si es de caracter discreto o digital, se le conoce como DFT (Discrete Fourier Transform).
En MATLAB, calcular la transformada de Fourier es tan sencillo como utilizar la funcion FFT (Fast Fourier Transform). Sin embargo, quizá no sea del todo claro cómo se ha de escoger el eje de coordenadas frecuenciales (eje X) para obtener una representación adecuada.
audio = audioread('audio.wav');
Fs = 16000;
L = length(audio);
NFFT = 2^nextpow2(L);
Y = fft(audio, NFFT)/L;
f = Fs/2*linspace(0,1,NFFT/2+1);
plot(f, 2*abs(Y(1:NFFT/2+1);
Comentemos línea a línea su significado.
audio = audioread('audio.wav');
Cargamos el archivo de audio en una variable llamada ‘audio’ de MATLAB.
Fs = 16000;
Introducimos la frecuencia de muestreo a la cual ha sido adquirido el audio. Es de vital importancia saber este parámetro, ya que de lo contrario no podremos identificar las frecuencias. Si por ejemplo has grabado el audio con un móvil, muchas aplicaciones permiten seleccionar la frecuencia de muestreo. Típicamente la frecuencia de muestro en un móvil es de 16 kHz, aunque para aseguraros podéis abrir el archivo con Audacity y os indicará la frecuencia de muestreo.
L = length(audio);
Calculamos el número de muestras que contiene el audio y lo guardamos en la variable L.
NFFT = 2^nextpow2(L);
La función fft() es más eficiente cuando calcula la transformada de Fourier de una función cuya longitud es una potencia de 2 (2, 4, 8, …). Por este motivo, vamos a calcular cuál es la potencia de 2 más próxima al número de muestras que contiene el audio. Si el archivo tiene 6 muestras, el número que le pasaremos a la función fft será 8, para que sea más eficiente. A este número lo llamaremos NFFT. Hay que tener en cuenta que este número será mayor que el número de muestras que contiene el archivo. Sin embargo, esto no afectará al resultado ya que las muestras que faltan son interpretadas como 0. De esta manera no añaden ningún contenido frecuencial al archivo original.
Y = fft(audio, NFFT)/L;
Calculamos la FFT con la función fft() cuyos argumentos son el audio que queremos transformar (audio), y el número de muestras sobre la que queremos que haga la transformada (NFFT). Dividimos entre L el resultado para normalizar los valores. La transformada la tendremos en la variable Y.
f = Fs/2*linspace(0,1,NFFT/2+1);
Ahora toca construir el eje de coordenadas. Las frecuencia que devuelve la FFt van de la frecuencia 0 hasta la frecuencia mitad de la frecuencia de muestreo \(\frac{F_s}{2}\) . Por tanto, necesitamos generar un vector que vaya desde 0 hasta \(\frac{F_s}{2}\). El número de elementos que este vector debe de contener es \(\frac{NFFT}{2}+1\) ya que debido a que la DFT genera una imagen espejo del espectro de frecuencia, solo querremos visualizar la mitad.
plot(f, 2*abs(Y(1:NFFT/2+1)));
Por último generamos la gráfica cuyo eje de coordenadas está contenido en la variable f y cuyo eje de ordenadas es 2 veces el valor absoluto (para mostrar solo la magnitud y no la parte real e imaginaria) de la mitad del espectro.
También podéis descargar el script audio_fft.m que he creado con función llamada audio_fft(audio, Fs) donde todo esto está ya encapsulado y que podéis descargar pulsando el enlace. Un ejemplo de uso sería:
audio_fft('archivo.wav', 16000);
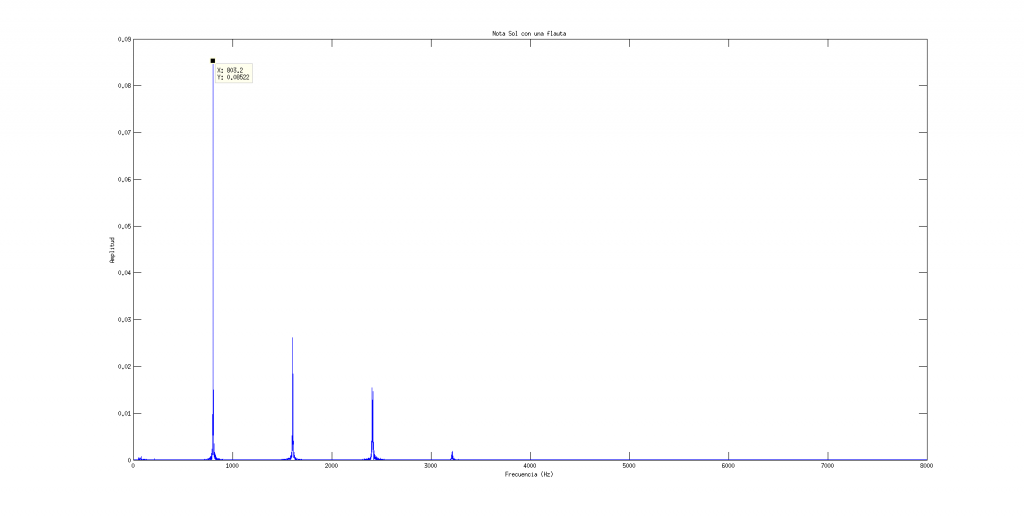
Como ejemplo he grabado un Sol con una flauta celta y he calculado el espectro frecuencial. El sonido es el siguiente:
Y el resultado es el siguiente:
Donde se puede apreciar claramente la frecuencia fundamental y sus armónicos.
Hola Rubén.
Gracias por tu post, me ayudo a aclarar mi construcción del eje de las frecuencias ya que tenia duda si era correcto o no.
En mi caso yo lo estoy construyendo de la siguiente forma
eje_f=((-Fs/2):(Fs/(length(x)-1)):(Fs/2));
dónde
Fs= frecuencia de muestreo.
x= señal original de audio.
y esta construido desde la mitad negativa de las frecuencias hasta la mitad positiva de las frecuencias ya que obtuve mi transformada de la siguiente manera:
X=fftshift(fft(x));
En mi caso, estoy gráficando las partes real e imaginaria en lugar de su módulo y el fftshift me sirve para centrar el espectro de frecuencias en 0.
Con tu imágen confirme que era correcto.
Saludos.
Hola Rubén, gracias por tu post. Tengo la siguiente duda: yo tengo una señal de audio, la cual quiero enventanar (cualquier tipo de ventana), hallar su fft pero aplicando el método de segmentación overlap-add. ¿Puedes ayudarme con eso?
Gracias.
hola manejando archivos de audio como se pueden extraer los picos del espectro?
Muchas gracias, me ayudo mucho en mi trabajo.