Series de Fourier

Una manera de representar una señal periódica, es mediante su serie de Fourier. La serie de Fourier de una función tiene la ventaja de expresar la misma función como una suma de senos y cosenos. Por ejemplo, una señal como un tren de pulsos, que tiene una expresión analítica poco rigurosa matematicamente hablando, se puede descomponer como suma senos y cosenos o lo que es lo mismo, sumas de exponenciales complejas.

Si tenemos una señal v(t) con un periodo \(T_0 = 1/f_0\) , su desarrollo en serie de Fourier exponencial es: \[v(t) = \sum_{n = -\infty}^{+\infty} c_n e^{j2\pi n f_0 t} ~~~~~ n = 0, 1, 2, …~~~(1)\]

Los coeficientes de la serie se pueden calcular como \(c_n = \int_{T_o} v(t) e^{-j2 \pi n f_0 t}dt\)

Una manera intuitiva de interpretar esta expresión, es pensar en el término \(c_n\) como el peso que tiene la frecuencia \(n\cdot f\) dentro de la señal v(t). De esta manera se promedia el producto \(v(t) e^{-j2 \pi n f_0 t}\) para todas las frecuencias.

Cabe destacar que \(c_n\) puede ser un (y normalmente son) números complejos, que se pueden expresar en forma polar como \(c_n = \left| c_n \right| e^{j~arg~c_n}\)

Otras consideraciones importantes son:

• Todas las frecuencias son multiplos enteros o armónicos de la frecuencia fundamental \(f_0 = 1/T_0\), por lo que la distancia entre líneas espectrales es uniforme.
• La componente continua es el valor promedio de la función.
• Si una función es real en tiempo, el espectro frecuencial tendrá simetría par para la amplitud e impar para la fase.

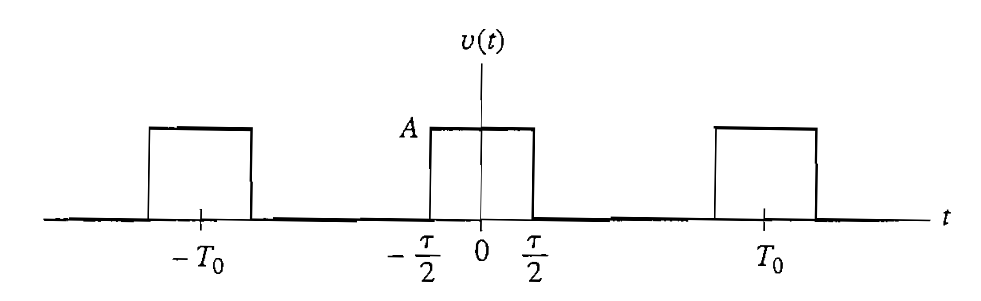
Para poner un ejemplo práctico, vamos ha calcular la serie de Fourier para un tren de pulsos rectangulares con periodicidad \(T_0\) cuya expresión analítica es:
\[ v(t)= \left\{\begin{matrix} A & \left|t \right| < \tau/2\\ 0 & \left|t \right| > \tau/2 \end{matrix}\right. \]

Aplicando la definición:
\[c_n = \frac{1}{T_0} \int_{-T_0/2}^{T_0/2} v(t) e^{-j2 \pi n f_0 t}dt = \frac{1}{T_0} \int_{-\tau/2}^{\tau/2} A e^{-j2 \pi n f_0 t}dt =\]\[= \frac{A}{-j2\pi n f_0 T_0} \left( e^{-j \pi n f_0 \tau} – e^{+j \pi n f_0 \tau}\right) = \frac{A}{T_0} \frac{\sin{\left( \pi n f_0 \tau \right)}}{n f_0 \tau} =\]\[= \frac{A}{T_0} sinc \left(n f_0 \tau\right)\]

Como hemos visto, si manipulamos la expresión de la serie de Fourier podemos llegar a una expresión compacta en la que aparece la función sinc.

Por tanto, si ahora fueramos capaces de generar los infinitos coeficientes \(c_n\), sustituyendolos en (1) seriamos capaces de reconstruir el tren de pulsos cuadrados a la perfección. Si por el contrario, solo calculamos un número finito de ellos, la función resultante tendría un aspecto parecido al de la imagen, donde se aprecia el fenómeno de Gibbs:

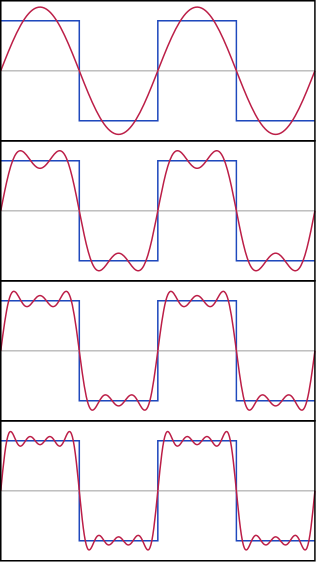
La animación anterior está implementada con la librería JavaScript P5.js. El código fuente es el siguiente:

let time = 0;
let path = [];
let slider;

function setup(){
	createCanvas(600, 400);
	slider = createSlider(0, 25, 3, 1);
	slider.position(20, 380);
}

function draw(){
	background(124,124,124);
	textSize(20);
	fill(255);
	text(' n = ' + slider.value(), width/2, 30);
	translate(200, 200);

	stroke(255);

	let x = 0;
	let prevx = 0;
	let y = 0;
	let prevy = 0;
	let c = color(255);

	for(let i = 0; i < slider.value(); i++){
		fill(c);
		stroke(255);
		let n = 2*i + 1;
		let amp = 100 * 4/(n * TWO_PI);
		x += amp * cos(n * time);
		y += amp * sin(n * time);
		// Point
		ellipse(x, y, 5);
		line(prevx, prevy, x, y);
		noFill();
		// Circle
		ellipse(prevx, prevy, amp * 2);
		prevx = x;
		prevy = y;
	}

	path.unshift(y);

	translate(200, 0);

	beginShape();
	for(let i = 0; i < path.length; i++){
		vertex(i, path[i]);
	}
	endShape();

	line(x-200, y, 0, path[0]);

	if(path.length > 200){
		path.pop();
	}

	time += 0.05;
}

Fuente: elaboración propia