Categoría: Electrónica

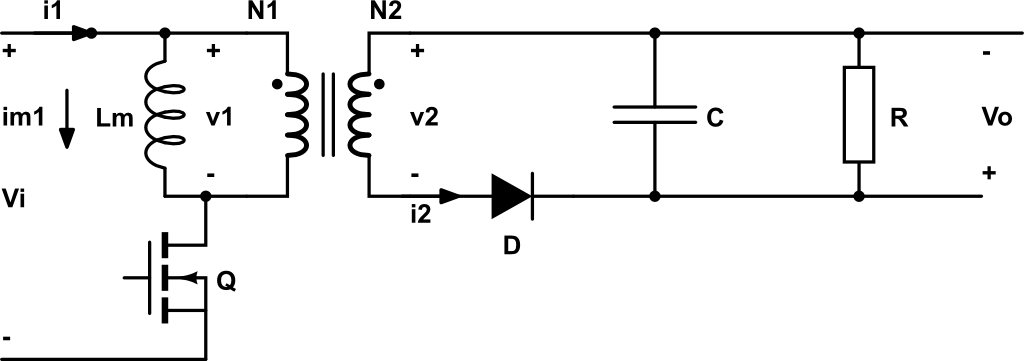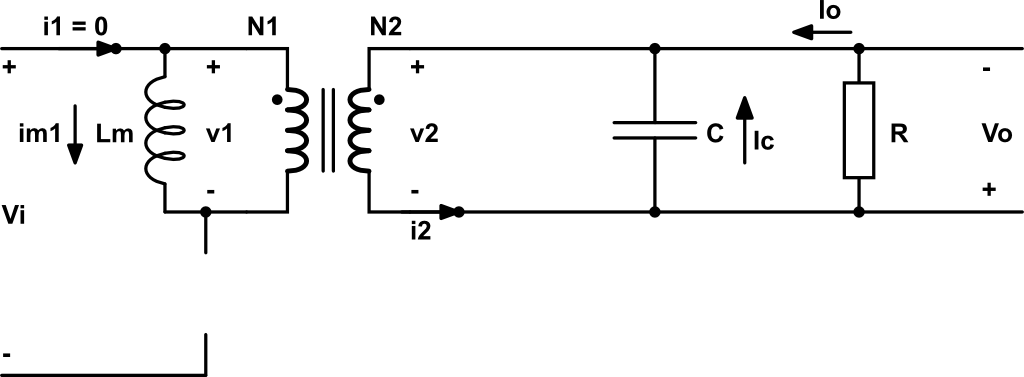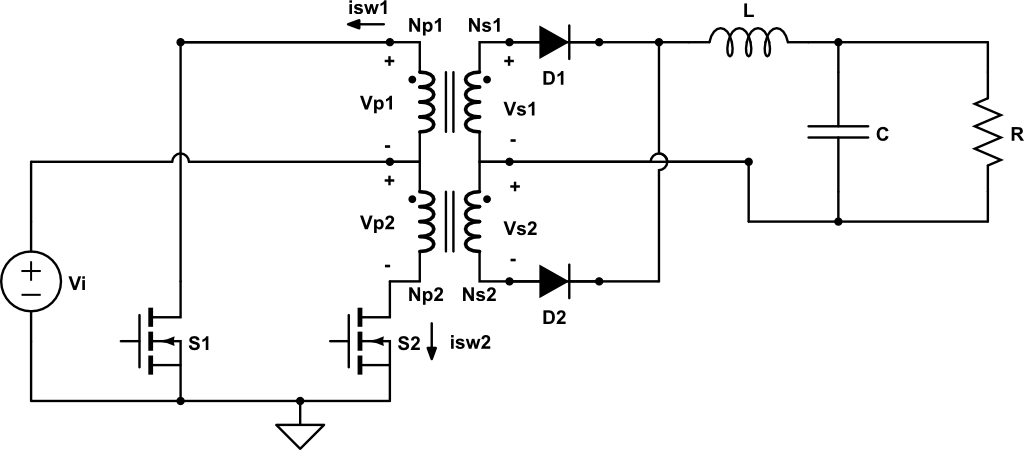
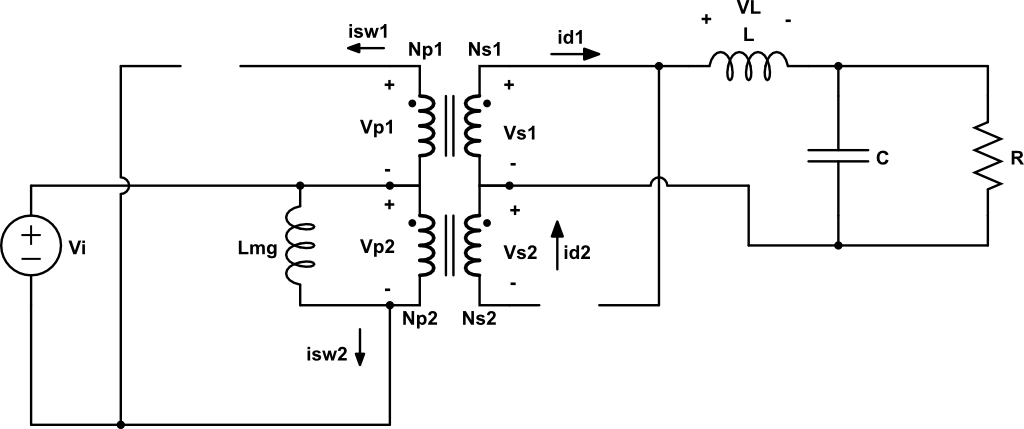
El convertidor push-pull trabaja en el primer y tercer cuadrante. Es decir, el transformador se magnetiza y se desmagnetiza en un periodo de trabajo. Está compuesto por una especie de inversor que convierte la tensión continua en «alterna» utilizando dos transistores y un rectificador de onda completa (transformador con toma intermedia y dos diodos) y un filtro paso bajo.

En este conversor tenemos 4 periodos de trabajo:

1. \(0<t<D T_s\): S1 ON, S2 OFF
2. \(D T_s<t<\frac{T_s}{2}\): S1 OFF, S2 OFF
3. \(\frac{T_s}{2}<t<\frac{T_s}{2} + D T_s\): S1 OFF, S2 ON
4. \(\frac{T_s}{2} + D T_s<t< T_s\): S1 OFF, S2 OFF

Intervalo 1: \(0<t<D T_s\): S1 ON, S2 OFF

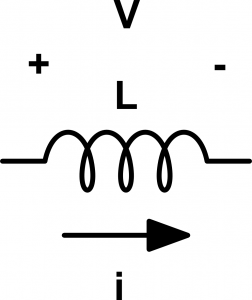
Tensión en el inductor

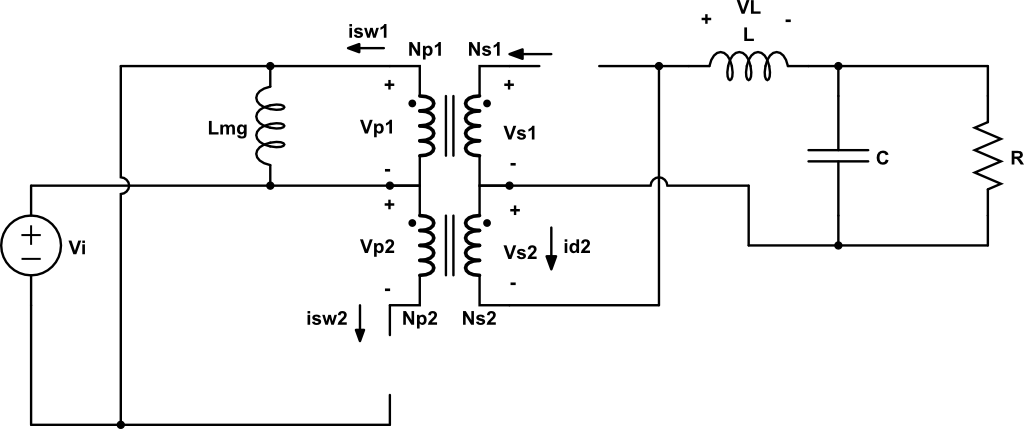
Haciendo el KCL en la malla 1 del primario, obtenemos:

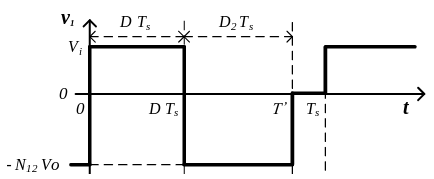
\[ -V_i – v_{p1} = 0 \Rightarrow v_{p1} = – V_i \]

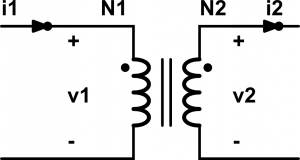
La tensión es negativa respecto a la referencia definida, por tanto la corriente irá en sentido contrario. La corriente «sale del punto», por tanto al otro lado del transformador «entrará por el punto». Esto hará que el diodo D1 no pueda conducir, quedando en circuito abierto mientras que el diodo D2 sí conducirá.

Teniendo en cuenta la relación de transformación:

\[ v_{s_2} = – \frac{N_{s2}}{N_{p1}} V_i \]

donde \(N_p = N_{p1} + N_{p2}\) y \(N_s = N_{s1} + N_{s2}\), en el que normalmente \( N_{p1} =N_{p2}  \) y \(N_{s1} = N_{s2} \) .

La tensión en el inductor:

\[ V_L = -v_{s_2} – V_o = \frac{N_{s2}}{N_{p1}} V_i – V_o \]

Corriente en el inductor

\[ V_L = L \frac{di_L}{dt} = \frac{N_{s2}}{N_{p1}} V_i – V_o \]

Si despejamos el diferencial de la corriente e integramos:

\[ i_L = I_{L_{min}} + \frac{1}{L} \left( \frac{V_i}{N_{ps}} – V_o \right) t  \]

Corriente de magnetización

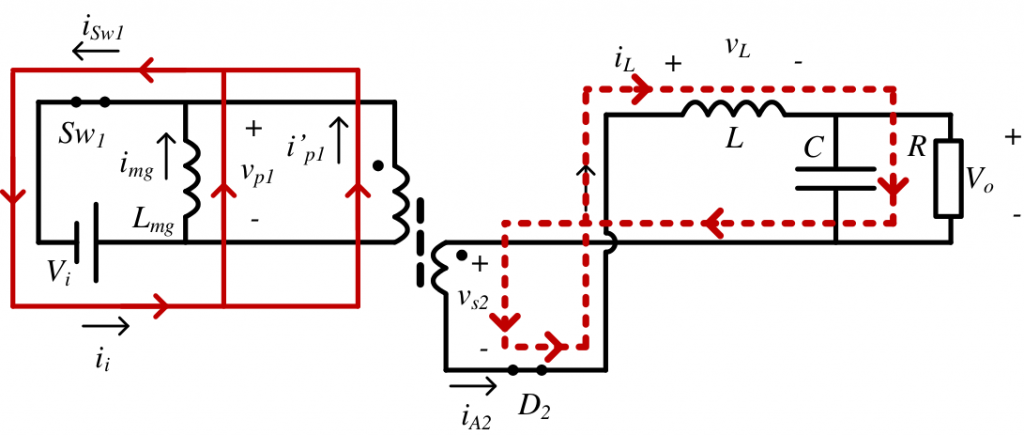
\[ i_{sw_1} = i_{mg} + \frac{i_L}{N_{ps}}\]

\[ i_{mg} = – I_{mg_{max}} + \frac{V_i}{L}t \]

\[ i_{mg}(0) = – I_{mg_{max}}\]

\[ i_{mg}(DT_s) =  I_{mg_{max}} =  I_{mg_{max}} + \frac{V_i}{L}DT_s \]

Intervalo 2: \(D T_s<t<\frac{T_s}{2}\): S1 OFF, S2 OFF

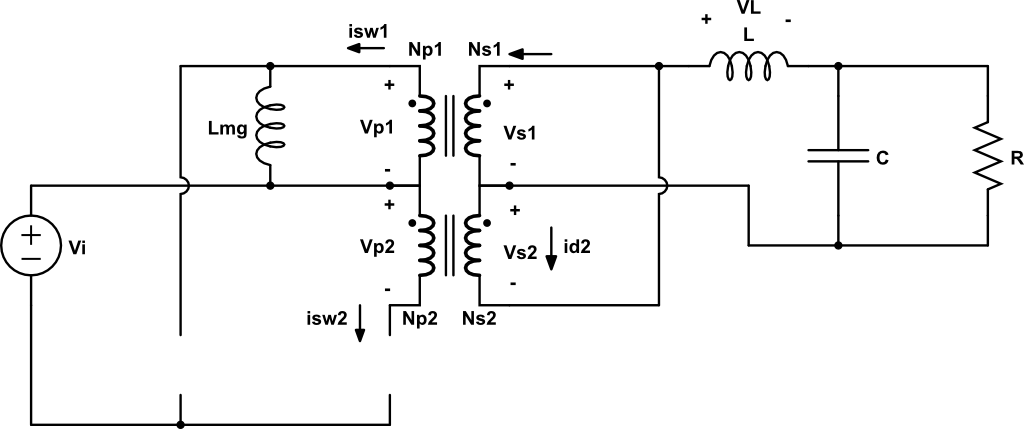
El flujo en el transformador (la corriente magnetizante) y la corrente en la inductancia del filtro de salida son variables de estado y por tanto no admiten discontinuidades. En el primario, puesto que ningún transistor conduce, este devanado está abierto y por lo tanto su corriente es nula (recuérdese que \(L_m\) no es más que un modelo para considerar la magnetización del núcleo, no debe confundirse \(i_m\) con una corriente real que circula por el primario).

En el secundario, la situación es más sutil, pero todo el problema se reduce a determinar qué diodos conduncen (esto es, \(D_1\), \(D_2\) o ambos a la vez) la corriente del inductor de salida.

Supongamos que \(D_1\) continua conduciendo y que \(D_2\) permanece bloqueado, es decir, únicamente conduce la mitad del secundario que está en serie con \(D_1\). Sabemos que la corriente en el inductor de salida y la corriente magnetizante del transformadr no adminten discontinuidades, pero además son variables independientes. Si se reduce la inductancia magnetizante al secundario y \(D_2\) no conduce, el resultado es similar a conectar dos inductancias en serie con condiciones iniciales de corriente distintas, lo que provocaría la sobretensión. Con los dos diodos en conducción, las inductancias magnetizantes y de filtro no están en serie y por lo tanto sus condiciones iniciales pueden ser cualesquiera.

La ecuación de la fuerza magnetomotriz dice:
La fuerza magnetomotriz se puede expresar como el producto del número de vueltas de cualquier devanado por la corriente magnetizante referida al devanado en cuestión y es igual a la suma de las corrientes si son entrantes en los «puntos» del transformador o la resta de las corrientes salientes de los puntos de cada toma, multiplicadas por su numero de vueltas correspondiente.

\[ \sum_{j=1}^{n} N_j i_j = N_1 \cdot i_1 = N_2 \cdot i_2 = … = N_n i_n = \epsilon \]

donde \( \epsilon\) es la fuerza magnetomotriz (que se define como \(F = N \cdot I\) y cuyas unidades son amperios-vuelta o Av).

Es decir, si tenemos un transformador con varias tomas, como es el caso, cada toma aportará un determinado flujo magnético dentro del núcleo del transformador. Según nuestro modelo del transformador utilizamos una inductancia ficticia que simula la corriente de magnetización. Para poder calcular la corriente que pasa en cada una de estas inductancias de magnetización, es necesario aplicar la ecuación de la fuerza magnetomotriz.

La ecuación de la fuerza magnetomotriz en el intervalo anterior es:

\[N_{s2} i_{D2}  – N_{p1} i_1 = N_{p1} i_{m} \]

En la que \( N_{p1} i_{m} \) no puede variar brucamente. Al hacer \(i_1 = 0\), debe de aparecer otra corriente (saliendo por el punto) que mantenga el transformador magnetizado, de manera que \(i_m\) no cambie bruscamente.

\[ N_{s2} i_{D2} – N_{s1} i_{D1} = N_{p1} i_m \]

Por tanto, se demuestra que \(D_1\) y \(D_2\) tienen que estar activos.

Para calcular la tensión en el inductor hay que tener varias cosas en consideración. Para que pueda circular corriente en el sentido en que lo hace \(i_{D1}\) e \(i_{D2}\), \(v_{s_1} = -v_{s_2}\) ya que la tensión del nodo común debe ser mayor que el del extremo del transformador. Por tanto:

\[v_{s_1} = -v_{s_2}\]

Debido a que el número de espiras entre el común y los extremos es el mismo, y el flujo magnético que pasa por ambas espiras es el mismo:

\[v_{s_1} = v_{s_2}\]

La única solución para que \(v_{s_1}\) y \(v_{s_2}\) cumplan estas condiciones es que \(v_{s_1} = 0\) y \(v_{s_2} = 0\).

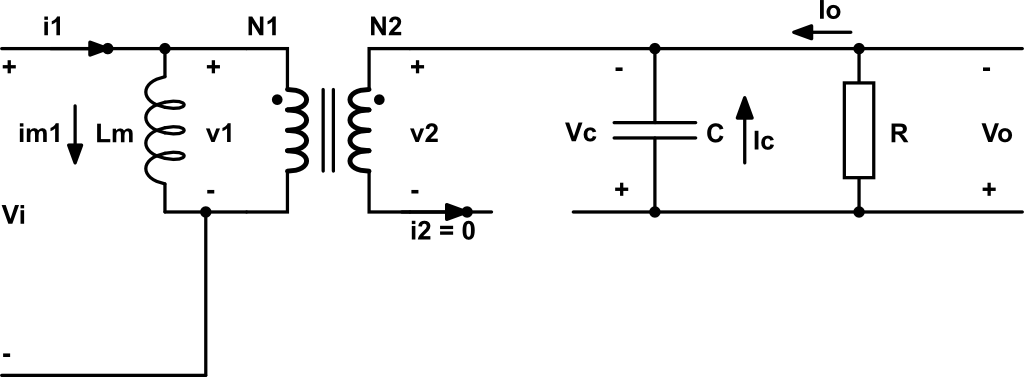
De esta manera, el circuito equivalente en el secundario es:

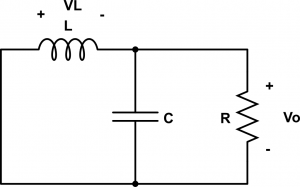
En el que \(V_L = -V_o\).

Corriente en el inductor

\[ V_L = L \frac{di_L}{dt} = -V_o \]

Si despejamos el diferencial de la corriente e integramos:

\[ i_L = I_{L_{max}} – \frac{1}{L} V_o \left( t- DT_s \right) t  \]

Corriente de magnetización

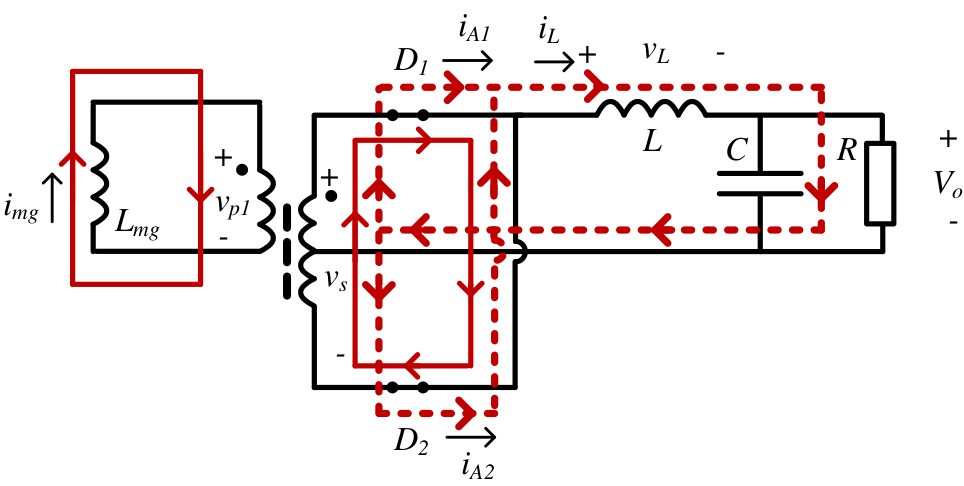
\[ v_s = 0 = v_p = v_{p_1} = 0 = L_{mg} \frac{di_{mg}}{dt} \]

\[ i_{A2} = \frac{i_L}{2} – \frac{i_{mg}}{2}N_{12} \]

\[ i_{A1} =\frac{i_L}{2} – \frac{i_{mg}}{2}N_{12} \]

\[ i_{mg_{1s}} = \frac{N_{p1}}{N_s} I_{mg_{max}} = \frac{N_{ps}}{2} I_{mg_{max}} \]

Intervalo 3: \(\frac{T_s}{2}<t<\frac{T_s}{2} + D T_s\): S1 OFF, S2 ON

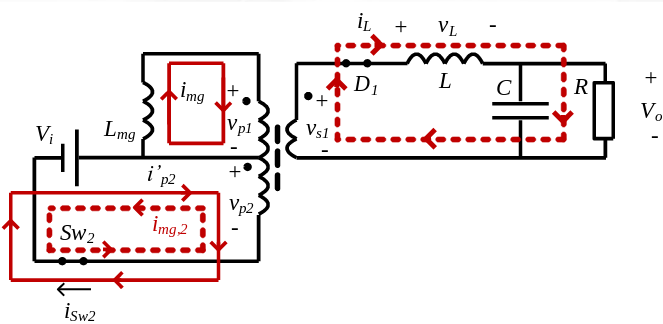
En este caso,

\[ v_{p2} = V_i\]

Ya que esta tensión es positiva, la corriente entrará por el punto en el primario y saldrá por el punto en el secundario. De manera que el diodo D1 estará en activa y diodo D2 estará en corte.

Del factor de transformación:

\[ v_{s_1} = \frac{N_{s_1}}{N_{p_2}} V_{p_2} = \frac{N_{s_1}}{N_{p_2}} V_{i} \]

Por lo que la tensión en el inductor es directamente:

\[ V_L = \frac{N_{s_1}}{N_{p_2}} V_{i} – V_o \]

Corriente en el inductor

La forma de onda de la corriente es exactamente igual que en el intervalo 1.

Corriente de magnetización

\[ i_{mg} = I_{mg_{max}} – \frac{V_i}{L_{mg}} \left(t – \frac{T_s}{2} \right) \]

\[ i_{sw_2} = \frac{1}{N_{ps}} i_L – i_{mg} \]

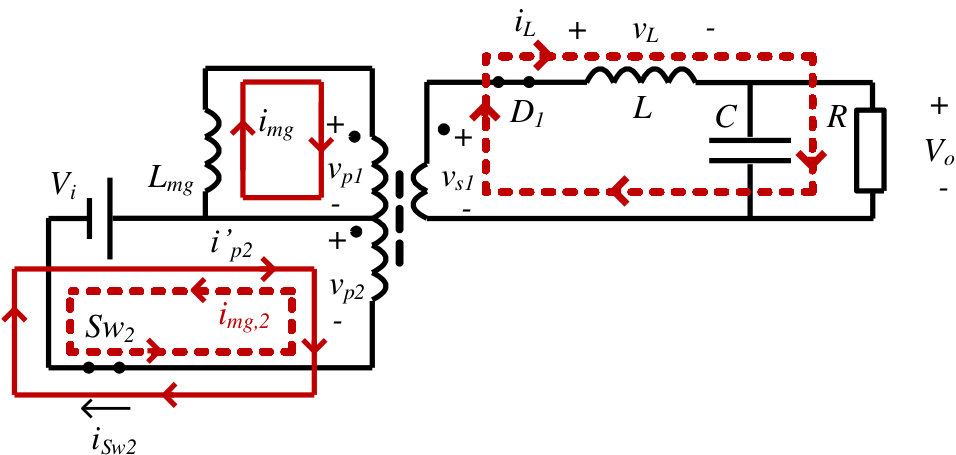
Intervalo 4: \(\frac{T_s}{2} + D T_s<t< T_s\): S1 OFF, S2 OFF

El intervalo 4 es exactamente igual al intervalo 2 ya que ambos transistores están de nuevo en OFF. Por tanto,

\[ V_L = -V_o \]

Corriente en el inductor

La forma de onda de la corriente es exactamente igual que en el intervalo 2.

Corriente de magnetización

\[ i_{mg} = – I_{mg_{max}} \]

\[ i_{mg_s} = \frac{N_{p1}}{N_s} \left( – I_{mg_{max}} \right) \]

\[ i_{A1} = \frac{I_L}{2} – \frac{N_{ps}}{2} I_{mg_{max}} \]

\[ i_{A2} = \frac{I_L}{2} + \frac{N_{ps}}{2} I_{mg_{max}} \]

Función de transferencia

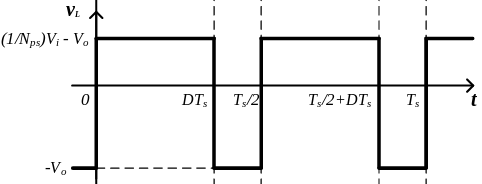
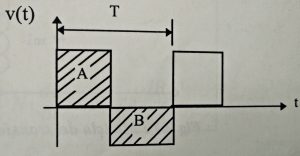
La media de la tensión en un inductor debe ser 0, ya que de lo contrario la corriente del inductor aumentaría indefinidamente. Forzando esta condición obtenemos la función de transferencia del convertidor:

\[ \left< V_L \right> = 0 = \frac{1}{\frac{T_s}{2}} \left[ \left( \frac{V_i}{N_{ps}} – V_o \right)DT_s – V_o \left( \frac{T_s}{2} – D T_s \right) \right] \]

\[ 0 =  D \frac{V_i}{N_{ps}} – V_o D-  \frac{V_o}{2} – D V_o \]

\[ V_o = \frac{2}{N_{ps}}DV_i \]

Donde \( 0 < D < 0.5 \) ya que no pueden estar ambos transistores en conducción simultaneamente.

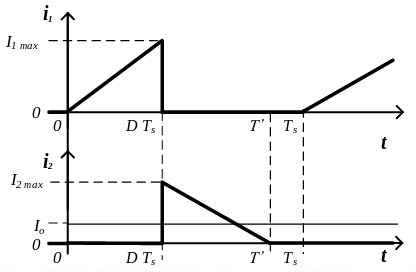
Corriente máxima y mínima en el inductor

De los intervalos 1 y 2 se han derivado las expresiones de la corriente en el inductor. Sin embargo, estas estaban en función de la corriente máxima y mínima que circula al final y principio de cada intervalo.

Para obtener la definición de corriente máxima y mínima tenemos que resolver un sistema de ecuaciones. Una de las ecuaciones nos la da la corriente media en el inductor y la otra, el rizado de la corriente en el inductor.

Corriente media en el inductor

Del circuito, aplicando el KCL podemos obtener que:

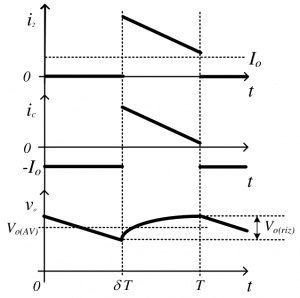
\[ i_L = i_c + I_o \]

Si calculamos el nivel medio de esta expresión:

\[ \left< i_L \right> = \left< i_c + I_o \right> = \left< i_c \right> + \left< I_o \right> = \left< I_o \right> = I_o\]

\( \left< i_c \right> = 0\) porque el nivel medio de la corriente en un condensador debe ser nulo por definición.

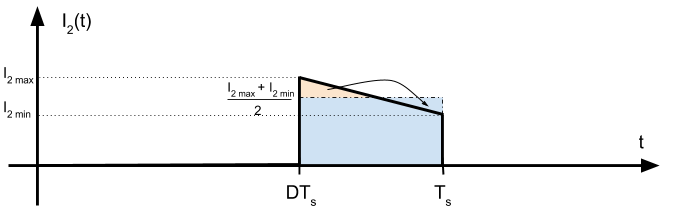
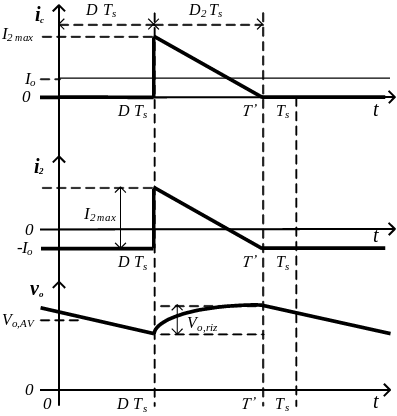
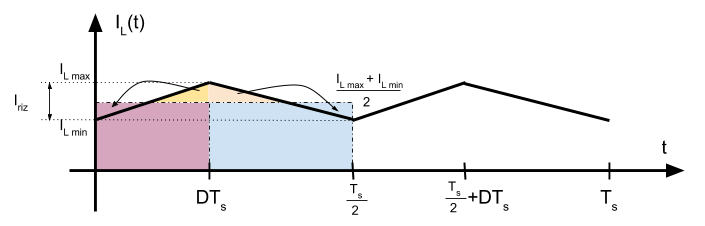
De la figura de la corriene en \( i_L \) podemos definir de manera alternativa el nivel medio de la corriente como:

\[ \left< i_L \right> = \frac{1}{\frac{T_s}{2}} \cdot \frac{T_s}{2} \frac{I_{L_{max}} + I_{L_{min}}}{2} = \frac{I_{L_{max}} + I_{L_{min}}}{2}\]

Por tanto, uniendo ambas expresiones obtenemos la primera de las ecuaciones del sistema:

\[I_o = \frac{I_{L_{max}} + I_{L_{min}}}{2}\]

Para la otra, definimos la corriente máxima (o mínima indistintamente) en función de la mínima (o máxima respectivamente). Para ello, decimos que \(I_{L_{max}} \) es \( I_{L_{min}}\) más el incremento de la corriente en ese intervalo, cosa que podemos hacer ya que conocemos la pendiente de la corriente (ver apartados anteriores).

\[ I_{L_{max}} = I_{L_{min}} + \frac{1}{L} \left( \frac{V_i}{N_{ps}} – V_o \right) D T_s \]

O del mismo modo:

\[ I_{L_{min}} = I_{L_{max}} – \frac{1}{L}  V_o \left( \frac{T_s}{2} – D T_s \right) \]

Despejando \( I_{L_{max}} – I_{L_{min}} \)

\[ I_{L_{max}} – I_{L_{min}} = \frac{1}{L} \left( \frac{V_i}{N_{ps}} – V_o \right) D T_s \]

Por tanto:

\[\left.\begin{matrix}
I_{L_{max}} + I_{L_{min}} = 2I_o \\
I_{L_{max}} – I_{L_{min}} = \frac{1}{L} \left( \frac{V_i}{N_{ps}} – V_o \right) D T_s
\end{matrix}\right\}\]

Resolviendo el sistema obtenemos que:

\[ I_{L_{max}} = I_o + \frac{1}{2L} \left( \frac{V_i}{N_{ps}} – V_o \right) D T_s \]

\[ I_{L_{min}} = I_o – \frac{1}{2L} \left( \frac{V_i}{N_{ps}} – V_o \right) D T_s \]

De \( I_{L_{min}} \) podemos calcular el límite de la conducción continua:

\[ I_{L_{min}} = I_o – \frac{1}{2L} \left( \frac{V_i}{N_{ps}} – V_o \right) D T_s = 0\]

Límite de la conducción continua:

\[ I_o = \frac{1}{2L} \left( \frac{V_i}{N_{ps}} – V_o \right) D T_s \]

 Corriente de magnetización en todo el periodo

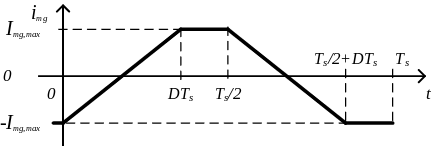
Como este convertidor magnetiza el núcleo de manera simétrica, podemos afirmar que \(I_{{mg}_{min}} = – I_{{mg}_{max}}\).

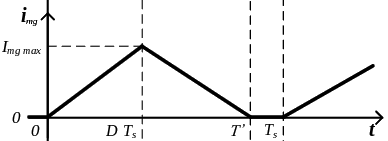
Para determinar el valor de \(I_{{mg}_{max}}\), hemos demostrado que en el primer periodo la tensión del primario es \(-V_i\). Por tanto, la inductancia de magnetización tiene aplicada una tensión de \(-V_i\), lo que fuerza a que haya una variación de corriente, tal y como vemos en la figura de arriba. En esta figura se ha tomado la dirección de la corriente de magnetización en sentido que va desde la toma central del transformador hasta la el otro extremo del transformador. Es por eso que tal y como vemos en la figura, al aplicar una tensión negativa la corriente aumenta.

La expresión de la corriente en este periodo será:

\[ i_{mg} = I_{{mg}_{min}}+ \frac{V_i}{L}t\]

En el instante \(t = DT_s\), el valor de la corriente es el máximo:

\[ I_{{mg}_{max}}= I_{{mg}_{min}} + + \frac{V_i}{L}DT_s\]

Como sabemos que \(I_{{mg}_{min}}= – I_{{mg}_{max}}\):

\[ I_{{mg}_{max}} = -I_{{mg}_{max}}  + \frac{V_i}{L}DT_s\]

\[ 2I_{{mg}_{max}} = \frac{V_i}{L}DT_s\]

\[ I_{{mg}_{max}} = \frac{V_i}{2L}DT_s\]

Si tenemos el valor del factor de inductancia \(A_L\) del núcleo, el número de vueltas del primario, la frecuencia de conmutación, el ciclo de trabajo y la tensión de entrada podemos calcular el valor máximo de la corriente de magnetización teniendo en cuenta que \( L_1 = \frac{N^2_1}{\mathfrak{R}} = N^2_1 A_L\). Por tanto:

\[ I_{{mg}_{max}} = \frac{V_i}{2 N^2_1 A_L}DT_s\]

Rizado de tensión de salida

Para calcular el rizado de tensión en la salida vamos a considerar la aproximación de que el rizado de corriente se va por el condensador y que el valor medio de la corriente se va por la carga:

\[ i_L \approx i_c + I_o\]

\[ i_c = i_L – I_o\]

La corriente en un condensador es \(i_c = C \frac{dv_c}{dt} \).

Por tanto, si integramos esta expresión obtenemos la tensión en bornes del condensador.

\[ v_c = \frac{1}{C} \int{i_c dt} \]

\[\left.v_c\right|^{v_{c,max}}_{v_{c,min}} = \frac{1}{C} \int_{t_1}^{t_2} i_c dt\]

El resultado de esta integral es igual al área marcada en naranja. Como es un triángulo, el área es \(\frac{1}{2} \text{base · altura} \) donde la base es la diferencia entre \(t_1\) y \(t_2\). Si vemos en el dibujo, es \(\frac{T_s}{4}\). Por tanto:

\[ \left.v_c\right|^{v_{c,max}}_{v_{c,min}} = \frac{1}{C} \frac{1}{2} \frac{T_s}{4} \frac{I_{riz}}{2} = \frac{1}{C} \frac{I_{riz}}{16 f_s} \]

 

Análisis en conducción continua

• Entre \(0 \leq t \leq D T_s\) Q: ON. \(i_1\) magnetiza el núcleo del transformador, por lo que genera un flujo magnético en el transformador. Este flujo magnético induce una tensión \(v_2\) que fuerza a que \(i_2\) tenga el sentido contrario al definido en el dibujo, es decir \(i_2 < 0\). Sin embargo, el diodo bloquea esta corriente, por que el diodo queda en circuito abierto (\(i_2 = 0\)).

En este caso, la tensión en el primario \(v_1\) es igual a \(V_i\).

\[v_1 = V_i = L_m \frac{di_{m1}}{dt} \Rightarrow \frac{di_{m1}}{dt} = \frac{V_i}{L_m} > 0 \rightarrow i_{m1} \text{ crece} \]

Despejando el diferencial de la corriente magnetizante del transformador:

\[ \int{\frac{di_{m1}}{dt} dt}= \int{\frac{V_i}{L_m} dt}\]

\[i_{m1}(t) = \frac{V_i}{L_m}t + I_{m_{min}} \]

\[v_2 = \frac{N_2}{N_1}v_1 = \frac{N_2}{N_1}V_i \]

\[ v_C = V_o\]

\[i_1 = i_{m1} + i_2 \cdot \frac{N_2}{N_1} = \left\{ i_2 = 0 \right\} = i_{m1}\]

\[i_2 = 0\]

\[i_c = C \frac{dv_0}{dt}  = – I_o \Rightarrow \frac{dv_0}{dt} = -\frac{I_o}{C} \rightarrow V_o\text{ decrece}\]

• Entre \(DT_s < t < T_s\). Q: OFF. El transistor está en circuito abierto y la corriente \(i_1 = 0\). La energía almacenada en el núcleo del transformador fuerza la conducción del diodo de salida debido a la corriente en sentido contrario que se induce de acuerdo con la ley de Lenz.

\[v_1 = \frac{N_1}{N_2}v_2 = L \frac{di_{m1}}{dt} = – \frac{N_1}{N_2} V_o \]

Despejando el diferencial de la corriente magnetizante del transformador:

\[ \int{\frac{di_{m}}{dt} dt} = \int{-\frac{N_1}{N_2}\frac{V_o}{L}dt} \]

\[ i_{m1}(t) = -\frac{N_1}{N_2} \frac{V_o}{L}\left( t-DT_s\right) + I_{m_{max}} \]

\[v_2 = -V_o \]

\[ v_c = V_o\]

\[ i_2 = i_c + I_o\]

\[ i_c = i_2 – I_0 = C \frac{dv_c}{dt} \]

De esta expresión, podemos despejar el diferencial de la tensión en el condensador. Solo es posible que el condensador se esté cargando en este periodo (\((1-D)T_s\)), por tanto, \(i_2 – I_o\) debe ser mayor que 0.

\[ \frac{dv_c}{dt} = \frac{i_2 – I_o}{C} > 0 \rightarrow v_c \text{ crece}\]

\[i_2 = \frac{N_1}{N_2}i_{m1}= \frac{N_1}{N_2} \left(-\frac{N_1}{N_2} \frac{V_o}{L}(t-DT_s) + I_{m_{max}} \right) = -\left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{L}(t-DT_s) + \left(\frac{N_1}{N_2}\right)^2 I_{m_{max}}\]

\[i_m(t)=\left\{\begin{matrix}\frac{V_i}{L}t+I_{m_{min}} &\text{si }0 < t < DT_s\\ -\frac{N_1}{N_2}\frac{V_o}{L}(t-DT_s)+I_{m_{max}} &\text{si }DT_s < t < T_s\end{matrix}\right. \]

Cómo calcular \(I_{2_{max}}\),  \(I_{2_{min}}\), \(I_{1_{max}}\) y  \(I_{1_{min}}\)

Para calcular \(I_{2_{max}}\) e \(I_{2_{min}}\) es necesario resolver un sistema de ecuaciones. La primera ecuación surge de considerar el nivel medio de \(i_2\).

\[ \left< i_2 \right> = \left< i_c + I_o \right> = \left< I_o \right> = I_o\]
Como en media la corriente del condensador debe de ser 0 (de lo contrario la tensión en sus bornes tendería a infinito), obtenenos que el nivel medio de \(i_2\) es \(I_o\).
También podemos calcular el nivel medio de \(i_2\) como:

\[ \left< i_2 \right> =  \frac{1}{T_s}\frac{I_{2_{max}}+I_{2_{min}}}{2}\left(1-D\right)T_s  =\frac{I_{2_{max}}+I_{2_{min}}}{2}\left(1-D\right) \]

Por tanto, igualando ambas expresiones:

\[\frac{I_{2_{max}}+I_{2_{min}}}{2}\left(1-D\right) = I_o \]

Y reescribiéndola, tenemos la primera ecuación del sistema:

\[I_{2_{max}}+I_{2_{min}}= \frac{2\cdot I_o}{\left(1-D\right) } \]

Para la segunda hay que tener en cuenta que cuando Q=OFF, \(i_2\) es \(\frac{N_1}{N_2}\) veces la corriente \(i_{m1}\). Si recordamos, \(i_{m1}\) sale de plantear la ecuación de la tensión del primario \(v_1\):

\[v_1 = \frac{N_1}{N_2}v_2 = L \frac{di_{m1}}{dt}\]

Y integrando esta ecuación obtenemos:

\[ i_{m1}(t) = -\frac{N_1}{N_2} \frac{V_o}{L}\left( t-DT_s\right) + I_{m_{max}} \]

Por tanto,

\[i_2 = -\left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{L}\left( t-DT_s\right) + I_{2_{max}} \]

Esta ecuación nos dice cómo es la pendiente de \(i_2\). Por lo que podemos definir \(I_{2_{min}}\) como \(I_{2_{max}}\) menos la pendiente de \(i_2\) durante el periodo \((1-D)T_s\):

\[ I_{2_{min}} = I_{2_{max}} -\left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{L} \left(1-D\right)T_s\]

Si despejamos la expresión \( I_{2_{max}}-I_{2_{min}}\), obtenemos:

\[ I_{2_{max}} -I_{2_{min}} = \left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{L} \left(1-D\right)T_s\]

Con lo que ya podemos resolver el sistema de ecuaciones:

\[ \left.\begin{matrix}
I_{2_{max}}+I_{2_{min}}= \frac{2\cdot I_o}{\left(1-D\right) } \\ I_{2_{max}} -I_{2_{min}} = \left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{L} \left(1-D\right)T_s
\end{matrix}\right\} \]

Y de aquí despejamos:

\[ I_{2_{max}} = \frac{I_o}{1-D} + \left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{2L_m}\left(1-D\right)T_s\]

\[ I_{2_{min}} = \frac{I_o}{1-D} – \left(\frac{N_1}{N_2}\right)^2 \frac{V_o}{2L_m}\left(1-D\right)T_s\]

Por último, teniendo en cuenta la ecuaciones que rigen el transformador, \(I_{1_{min}} = \frac{N_2}{N_1} I_{2_{min}}\) y \(I_{1_{max}} = \frac{N_2}{N_1} I_{2_{max}}\), por lo tanto:

\[ I_{1_{max}} = \frac{N_2}{N_1} \frac{I_o}{1-D} +\frac{N_1}{N_2} \frac{V_o}{2L_m}\left(1-D\right)T_s \]

\[ I_{1_{min}} = \frac{N_2}{N_1} \frac{I_o}{1-D} -\frac{N_1}{N_2}\frac{V_o}{2L_m}\left(1-D\right)T_s \]

También podemos escribir \(I_{1_{min}} \) e \(I_{1_{max}}\) en función de \(V_i\) sustituyendo \(V_o = \frac{N_2}{N_1}\frac{V_i D}{L}\).

\[ I_{1_{max}} = \frac{N_2}{N_1} \frac{I_o}{1-D} +\frac{V_i}{2L_m}D T_s \]

\[ I_{1_{max}} = \frac{N_2}{N_1} \frac{I_o}{1-D} -\frac{V_i}{2L_m}D T_s \]

Rizado de salida

Para calcular el rizado, hay que tener en cuenta la corriente del condensador ya que será el responsable de filtrar dicho rizado.

También vamos a considerar que la tensión de salida \(v_o\) está compuesta por la tensión DC y el rizado de la siguiente manera:

\[v_o = V_{o~DC} + v_{o~riz}\]

A priori ya podemos suponer, que cuanto mayor sea el valor de la capacidad C del condensador menor será el rizado.

Cuando Q=ON, \(i_c = -I_o\).

Por lo que podemos integrar la corriente del condensador en el primer intervalo:

\[ v_c = \frac{1}{C}\int_0^{DT_s}{i_c(t) dt} = \frac{1}{C} \int_0^{DT_s}{-I_o dt} = – \frac{1}{C} I_o D T_s\]

De aquí, obtenemos que la variación del rizado es:

\[\Delta V_{o~riz} = \frac{1}{C} I_o D T_s \]

También hay que considerar que debido a la ESR del condensador, habrá una fuga en corriente que no irá hacia la carga sino que se quedará en el condensador. Esta tensión es:

\[V_{o~riz~(ESR)} = I_{2_{max}} \cdot ESR \]

Análisis de conducción discontinua

En conversor Flyback entra en conducción discontinua cuando el núcleo magnético del transformador se desmagnetiza. Esto ocurre cuando \(I_{mg_{min}}\) o su equivalente reflejado en el secundario \(I_{2_{min}}\) es 0.

\[I_{2_{min}} = 0 = \frac{I_o}{1-D} – \frac{N_1^2}{N_2^2}\frac{V_o}{2L} \left( 1 -D\right) T_s \]

En el periodo \(0 \leq t \leq D T_s\) el núcleo se magnetiza pero la energía que almacena no es la suficiente para que pasado el segundo periodo todavía quede algo de densidad de flujo magnético en el núcleo (magnetización). Por eso en el momento T’ del segundo periodo \(DT_s < t < T_s\), la corriente \(I_2\) se hace 0. Como tampoco hay tensión aplicada sobre el primario, la tensión en primario y secundario es 0.

Para sacar la función de transferencia del conversor Flyback en conducción discontinua debemos resolver un sistema de ecuaciones. La primera ecuación la podemos encontrar haciendo la media de la tensión en el primario y despejando \(D_2\).

Como la media de la tensión en una bobina debe de ser 0, podemos encontrar la relación entre \(D_2\) y el resto de parámetros.

\[ \frac{1}{T_s} \left[V_i D T_s + \left(- \frac{N_1}{N_2} V_o D_2 T_s \right) \right] = 0 \]

\[ D_2 = \frac{V_i D}{N_{12} V_o } ~~~(1)\]

La otra ecuación la obtenemos de igualar la media de la corriente \(i_2\) con \(I_o\)

\[ I_o = \frac{V_o}{R} = \frac{1}{T_s} \left( D_2 T_s \frac{1}{2} N_{12} I_{mg_{max}} \right)~~~(2)\]

Al estar en conducción discontinua, \(I_{mg_{max}} \) es directamente:

\[I_{mg_{max}}  = \frac{V_i}{L} D T_s ~~~(3)\]

Sustituyendo (1) y (3) en (2), obtenemos:

\[  V_o = \sqrt{\frac{R T_s}{2L}}D V_i = \sqrt{\frac{1}{2 \tau_s}} D V_i\]

En el que \(\tau_s\) es:

\[ \tau_s = \frac{L}{R T_s} \]

Por tanto, el conversor Flyback en conducción continua se comporta como un buck-boost en el que podemos conseguir tanto tensiones mayores como menores a la de entrada mientras que en conducción discontinua se comporta como un buck. Es decir, solo se pueden conseguir tensiones de salida menores a la de entrada.

Rizado de salida

En conducción discontinua el rizado de salida se calcula de la misma forma que en conducción continua, con la diferencia de que la corriente que pasa por el condensador ahora es menor. Por tanto, tanto el rizado debido a la capacidad como por la ESR es menor.

Como ya sabemos, \( i_c = i_2 – I_o\). Y la diferencia de tensión entre dos tiempos \(t_0\) y \(t_1\) es:

\[ \Delta v_c = \frac{1}{C} \int_{t_0}^{t_1}{i_c~dt} \]

Al estar en conducción discontinua podemos obtener fácilmente la expresión analítica de \(i_2\):

\[ i_2 = I_{2_{max}} – \frac{N_1^2}{N_2^2} \frac{V_o}{L} \left(t-DT_s\right) \]

Donde \( I_{2_{max}} \) es:

\[ I_{2_{max}} = \frac{N_1}{N_2} \frac{V_i}{L} D T_s \]

De \(i_2\) podemos obtener cuándo la corriente se hace 0, es decir T’:

\[i_2 = I_{2_{max}} – \frac{N_1^2}{N_2^2} \frac{V_o}{L} \left(T’-DT_s\right)=0 \]

\[ T’ = \left( \frac{V_i}{N_{12}} + 1\right) \frac{DT_s}{V_o} \]

Por tanto, ya podemos calcular el rizado de tensión debido a la capacidad:

\[ \Delta v_c = \frac{1}{C} \int_{DT_s}^{ \left( \frac{V_i}{N_{12}} + 1\right) \frac{DT_s}{V_o}}{\left[I_{2_{max}} – \frac{N_1^2}{N_2^2} \frac{V_o}{L} \left(t-DT_s\right) \right]~dt} \]

O de manera más sencilla, teniendo en cuenta los periodos en los que \(i_c = -I_o\).

\[ \Delta v_c = \frac{1}{C}\left( \int_{0}^{DT_s}{i_c~dt} + \int_{T’}^{T_s}{i_c~dt} \right) = \frac{1}{C}\left( \int_{0}^{DT_s}{-I_o} + \int_{T’}^{T_s}{-I_o} \right) \]

\[ \Delta v_c = \frac{1}{C} \left(-I_o\right) \left( DT_s + T_s – T’\right) \]

\[ \Delta v_c = \frac{1}{C} \left(-I_o\right) \left[ D + 1 – \left( \frac{V_i}{N_{12}} + 1\right) \frac{D}{V_o}\right]T_s \]

De acuerdo con la ley de Faraday,

\[ v_1 = N_1 \frac{d\Phi}{dt} \]

\[ v_2 = N_2 \frac{d\Phi}{dt} \]

de lo que puede derivarse que:

\[ \frac{v_1}{v_2} = \frac{N_1 \frac{d\Phi}{dt}}{ N_2 \frac{d\Phi}{dt}}  = \frac{N_1}{N_2} \]

Por lo que el cociente entre espiras determina la relación entre las tensiones de los devanados.

Si se considera una reluctancia nula, es decir, un transformador ideal, la relación de corrientes es:

\[N_1 \cdot i_1 – N_2 \cdot i_2 = 0 \]

Si por el contrario la reluctancia no es nula y se tiene en cuenta el fenómeno de saturación:

\[N_1 \cdot i_1 – N_2 \cdot i_2 =  \mathscr{R} \cdot \Phi \]

La inductancia magnetizante vista desde el primario es:

\[\frac{N^2_i}{\mathscr{R}} = L_{m1} \]

 

En el análisis de mallas no importa qué criterio se utilice a la hora de definir la polaridad de las tensiones mientras se haga en todo el circuito con el mismo.

Por ejemplo, considerando que si la flecha entra por (-), la tensión es negativa:

\[ -V_1 – V_2 = 0 \]

\[ V_1 = -V_2 \]

\[V_L(t) = L \frac{di(t)}{dt} \]

Si despejamos el diferencial e integramos:

\[\frac{di(t)}{dt} = \frac{V_L}{L}\]

\[\int{\frac{di(t)}{dt} dt} = \int{\frac{V_L}{L} dt}\]

\[ i(t) = \int{\frac{V_L}{L} dt} =  i(0) + \frac{V_L}{L}t \]

La variación de la corriente en el tiempo no puede ser instantánea, ya que de lo contrario habría un pico infinito de tensión en el inductor (\(v(t) = \infty\)).

\[ \frac{di(t)}{dt} \neq \infty \]

Si el valor de la inductancia L es grande, las variaciones de corriente en el inductor serán pequeñas, por lo que el inductor se podrá considera como una fuente de corriente.

En régimen permanente, el valor medio de la tensión en los extremos del inductor debe ser nulo, ya que de lo contrario la corriente en bornes del inductor aumenaría hasta el infinito.

Es decir, ya que:

\[ i(t) = \int_0^t{-\frac{v_L(t)}{L} dt} \]

si \(v_L(t)\) no tuviese una media nula, la integral de la tensión sería infinito, ya que solo sumaría.

Por tanto:

\[<v(t)> = \frac{1}{T} \int_0^T v(t) dt = 0\]

El polo positivo de la fuente de tensión equivalente que modela el efecto de la polarización de la unión PN está en el mismo lado que el ánodo (positivo).

Cuando hablamos del comportamiento de un condensador en frecuencia, imaginamos que su impedancia decrece hasta hacerse 0 en el infinito.

Sin embargo, en la realidad nos encontramos que el modelo real de una condensador tiene una resistencia en serie además de un inductor. En esta entrada vamos a ver solo los efectos que tiene dicha resistencia en serie, también conocida como ESR (equivalent series resistor).

Caso ideal

Si calculamos la función de transferencia de este circuito, encontraremos que tiene la siguiente expresión:
\[H(s) = \frac{\frac{1}{CR_g}}{s+\frac{1}{CR_g}}\]

Vemos que la frecuencia de corte a la cual el valor absoluto de la función de transferencia H(s) ha disminuido 3 dB es:
\[f = \frac{1}{2\pi R C} = \frac{1}{2\pi \cdot 50 \cdot 10^{-6}} = 3183 Hz\]

Sin embargo, ¿cómo va a ser su respuesta en frecuencia si añadimos una resistencia en serie?

Caso real

Para tener en cuenta los efectos de la resistencia en serie, modificamos el esquemático original añadiendo la resistencia en serie con el condensador. Para que los efectos sean más notables de manera que se vean mejor las consecuencias que tiene, el valor de la resistencia se ha escogido alto (50 Ω). Sin embargo, los condensadores reales intentan mantener este valor tan bajo como sea posible para seguir manteniendo las características de condensador en un ancho de banda más amplio.

La función de transferencia de este circuito es:
\[H(s) = \frac{R_L}{R_g + R_L}\frac{s+ \frac{1}{C R_L}}{s+ \frac{1}{C \left( R_L + R_g \right)}}\]

Como vemos, la función de transferencia tiene un cero en \(f_c = \frac{1}{2 \pi C R_L}\) y polo en \(f_p = \frac{1}{2\pi C \left( R_L + R_g\right) }\). El cero fuerza un pendiente a partir de \(f_1\) de -20 dB/dec, mientras que el polo fuerza una pendiente de +20 dB/dec a partir de \(f_2\), tal y como vemos en el diagrama de bode:

Como vemos, el cero anula al polo de manera que la respuesta en frecuencia es plana para altas frecuencias (en la realidad el inductor en serie hace que aumente. Sin embargo, ahora no se están contemplando sus efectos). La frecuencia del polo está por debajo de la frecuencia del cero \(f_p < f_c\). Además, la frecuencia del cero está determinada por el valor de la resistencia en serie y por el valor del condensador. Por tanto, si hacemos \(R_L\)muy pequeña, estaremos retardando el efecto del cero y con ello, haciendo que la respuesta frecuencial del condensador sea igual a la del caso ideal en un ancho de banda mayor.

Si hacemos \(R_L = 0.01 \Omega\), las características de condensador (disminución de impedancia al incrementar la frecuencia) se dan para un ancho de banda mayor:

A modo de comparativa, podemos observar las diferencias mejor si superponemos todos los diagramas de bode.

El script de MATLAB utilizado para simular y hacer estas gráficas es:

clear all;
close all;
 
s = tf('s');
Rg = 50;
RL = 50;
RLow = 0.01;
C = 1e-6;
 
%% Con ESR
H1 = ((1+s*C*RL)/(s*C*(Rg+RL)+1));
 
%% Sin ESR
H2 = (1/(C*Rg))/(s+1/(C*Rg));
 
%% Con bajo ESR
H3 = ((1+s*C*RLow)/(s*C*(Rg+RLow)+1));
 
bode1 = bodeplot(H1,'r',H2,'b--', H3, 'g-.');
 
setoptions(bode1, 'FreqUnits', 'Hz');
 
legend('Circuito RC con alta ESR', 'Circuito RC ideal', 'Circuito RC con baja ESR');
grid on;

Conclusión

Como vemos, debido a efectos parásitos como la resistencia en serie (ESR), el condensador deja de comportarse como tal a partir de una determinada frecuencia. Por debajo de ella, el condensador puede ser utilizado como tal. En los datasheets, este parámetro viene expresado como ESR aunque generalmente, se engloba dentro de un parámetro más general que es el factor de calidad Q.

Hace poco escribía sobre la importancia de tener en cuenta la resistencia parásita serie de un condensador (ESR). La ESR es un parámetro importante pero sin embargo, no tener en cuenta la inductancia serie equivalente puede ser incluso más catastrófico en un diseño.

Como ya habíamos hablado, estos elementos parásitos inherentes al condesador real hacen que su comportamiento deje de ser el esperado. La expresión de la impedancia de un condensador es
\[Z_C = \frac{1}{2 \pi f C}\]
Por lo que al subir en frecuencia su impedancia disminuye.

Podemos ver que hay un tanque LC en serie (un condensador y un inductor en serie). La característica principal de un tanque LC en serie es que a su frecuencia de resonancia, \(f_0 = \frac{1}{2\pi \sqrt{LC}}\) se comporta como un cortocircuito. Por debajo de esa frecuencia, predomina la impedancia del condesador, por encima de la frecuencia de resonancia domina la impedancia del inductor y justo a la frecuencia de resonancia la impedancia del condensador es igual y de signo contrario a la del inductor. Es por ello que se anulan.

Debido a esto, podemos esperar que a la frecuencia de resonancia la salida sea 0 porque ambas impedancias se anulen cortocircuitando la salida a masa.

La función de transferencia de este circuito (o parámetro S21) es:
\[H(s) = \frac{s^2 + \frac{1}{LC}}{s^2 + s \frac{R_g}{L} + \frac{1}{LC}}\]

De la gráfica podemos observar todo lo que habíamos predicho teóricamente.

Sin embargo, si añadimos la ESR encontramos que la función de transferencia ahora es
\[H(s) = \frac{s^2 + s \frac{R}{L} + \frac{1}{LC}}{s^2 + s \frac{R+R_g}{L} + \frac{1}{LC}}\]

Como se puede ver, cuanto más grande es la ESR el pico de resonancia es menor. Si un condensador es muy malo (tiene unas ESR y ESL altas), se parecerá más a la curva azul (ESR = 10).

Los transformadores son elementos muy útiles cuando es necesario modificar la impedancia vista desde un punto del circuito. Cuando estamos diseñando un filtro paso banda y queremos conectar la siguiente etapa es muy importante no modificar la resistencia del circuito, ya que modificaríamos su ancho de banda. Por otra parte, construir transformadores es algo caro, que ocupa mucho espacio y poco práctico. Por ello intentar buscar una solución sin que utilice bobinas es una buena idea.

Transformación paralelo-serie

Para empezar, deberemos saber como pasar del paralelo de una resistencia y un condensador a la disposición en serie de una resistencia y un condensador:

 

La impedancia equivalente del paralelo es:

\[Z = \frac{R_p}{1 + R_p C_p j \omega} = \frac{R_p}{1+R_p C_p j \omega} \cdot \frac{1-j\omega R_p C_p}{1-j\omega R_p C_p}=\frac{R_p(1-j\omega R_p C_p)}{1+\omega^2 R_p^2 C_p^2}=\frac{R_p}{1+\omega^2 R_p^2 C_p^2} – \frac{j\omega R_p^2 C_p}{1+\omega^2 R_p^2 C_p^2}\]

Si \(R_p >> \frac{1}{C_p\omega}\), entonces podemos aproximar la impedancia equivalente como:

\[Z \approx \frac{1}{R_p C_p^2 \omega^2}-j\frac{1}{\omega\cdot C_p}\]

Por tanto:

\[R_s = \frac{1}{R_p C_p^2 \omega^2}\]

\[C_s = C_p\]

Como hemos visto esto solo es válido cuando la impedancia de la resistencia paralela es mucho mayor que la impendancia del condensador. Por tanto, podemos reescribir la condición como \[f >> \frac{1}{2\pi R_p C_p}\]

Veamos un ejemplo:

 

Primero tenemos que comprobar que a la frecuencia de trabajo (27 MHz) se cumplen la condición necesaria para que la aproximación sea válida:

\[f >> \frac{1}{2\pi R_p C_p} = \frac{1}{2\pi 1k\Omega 1nF}=159 kHz\]

Como vemos, a 27 MHz cumplimos de sobra la condición. Para calcular \[C_s\]:

\[R_s = \frac{1}{R_p C_p^2 \omega^2} = \frac{1}{1 k\Omega (1nF)^2 (2\pi\cdot 27 MHz)^2}=0.0347 \Omega\]

Transformación serie-paralelo

De la misma manera, podemos transformar el circuito serie en paralelo.

 

Ahora las identidades son:

\[R_p = \frac{1}{R_s C_s^2 \omega^2}\]

\[C_p = C_s\]

Siempre y cuando \[f >> \frac{1}{2\pi R_p C_p}\]

Uso como transfomador

 

Como vemos, de esta manera conseguimos tener un condensador y una resistencia en paralelo del valor:

\[C_{eq}=\frac{C_1\cdot C_2}{C_1 + C_2}\]

\[R_p = R_0 (1+\frac{C_2}{C_1})^2\]

Como vemos \((1+\frac{C_2}{C_1})^2\) veces más grande.

Los filtros son una de las piezas claves en la electrónica y sobretodo en el mundo de las telecomunicaciones. Para poder identificar el orden de un filtro, si trazamos si diagrama de Bode y observamos que la atenuación es de 20 dB/década se tratará de un filtro de 1º orden, 40 dB/década para un filtro de 2º orden, 60 dB/decada para un filtro de 3º orden, etc. Otra manera más práctica es mirar el número de polos y ceros que presenta la función de transferencia, lo que se traduce en mirar cuántos condensadores y inductores presenta. Esta regla no tiene por qué ser siempre cierta, así que para asegurarnos será mejor recurrir al diagrama de Bode.

En esta ocasión nos centraremos en los filtros de segundo orden, en concreto los filtros paso bajo. Su función de transferencia genérica es de la forma:
\[H(s)=\frac{H_0}{s^2+2\zeta\omega_0 s+\omega_0^2}\]

\(H_0\): es la amplificación a baja frecuencia del filtro
\(\zeta\): es el coeficiente de amortiguación
\(BW\)) en radianes. Por tanto la función de transferencia puede ser reescrita como:
\[H(s)=\frac{H_0}{s^2+BW s+\omega_0^2}\]
Otro parámetro importante de un filtro paso banda es el factor de calidad. Este nos da información sobre como de estrecho y selectivo es el filtro. Una de las definiciones del factor de calidad (Q) es:
\[Q=\frac{f_o}{BW}\]
Si lo analizamos asintoticamente, si el filtro tuviera un ancho de banda \(f_0 \pm BW\), pero como veremos es algo muy complicado de conseguir actualmente.